要素ライブラリおよび材料データ
要素ライブラリおよび材料データ
要素ライブラリ
FrontISTRは、表 4.1.1に示す要素群を解析に使用することができる。 FrontISTRはメッシュデータをHEC-MWを使用して入力するので、以下の要素ライブラリの記述はHEC-MWの説明に準じたものである。 要素ライブラリを図 4.1.1に、要素コネクティビティおよび面番号の定義を 図 4.1.2に示す。
表 4.1.1 要素ライブラリ一覧
| 要素種類 | 要素番号 | 説明 |
|---|---|---|
| 線要素 | 111 | 2節点リンク要素 |
| 112 | 3節点リンク要素 | |
| 平面要素 | 231 | 3節点三角形要素 |
| 232 | 6節点三角形二次要素 | |
| 241 | 4節点四角形要素 | |
| 242 | 8節点四角形二次要素 | |
| ソリッド要素 | 301 | 2節点トラス要素 |
| 341 | 4節点四面体要素 | |
| 342 | 10節点四面体二次要素 | |
| 351 | 6節点五面体要素 | |
| 352 | 15節点五面体二次要素 | |
| 361 | 8節点六面体要素 | |
| 362 | 20節点六面体二次要素 | |
| インターフェース要素 | 541 | 四角形断面一次要素 |
| 542 | 四角形断面二次要素 | |
| 梁要素 | 611 | 2節点梁要素 |
| 641 | 2節点梁要素(3自由度節点4点による) | |
| シェル要素 | 731 | 3節点三次元一次要素 |
| 732 | 6節点三次元二次要素 | |
| 741 | 4節点三次元一次要素 | |
| 743 | 9節点三次元二次要素 | |
| 761 | 3節点三次元一次要素(3自由度節点6点による) | |
| 781 | 4節点三次元一次要素(3自由度節点8点による) |
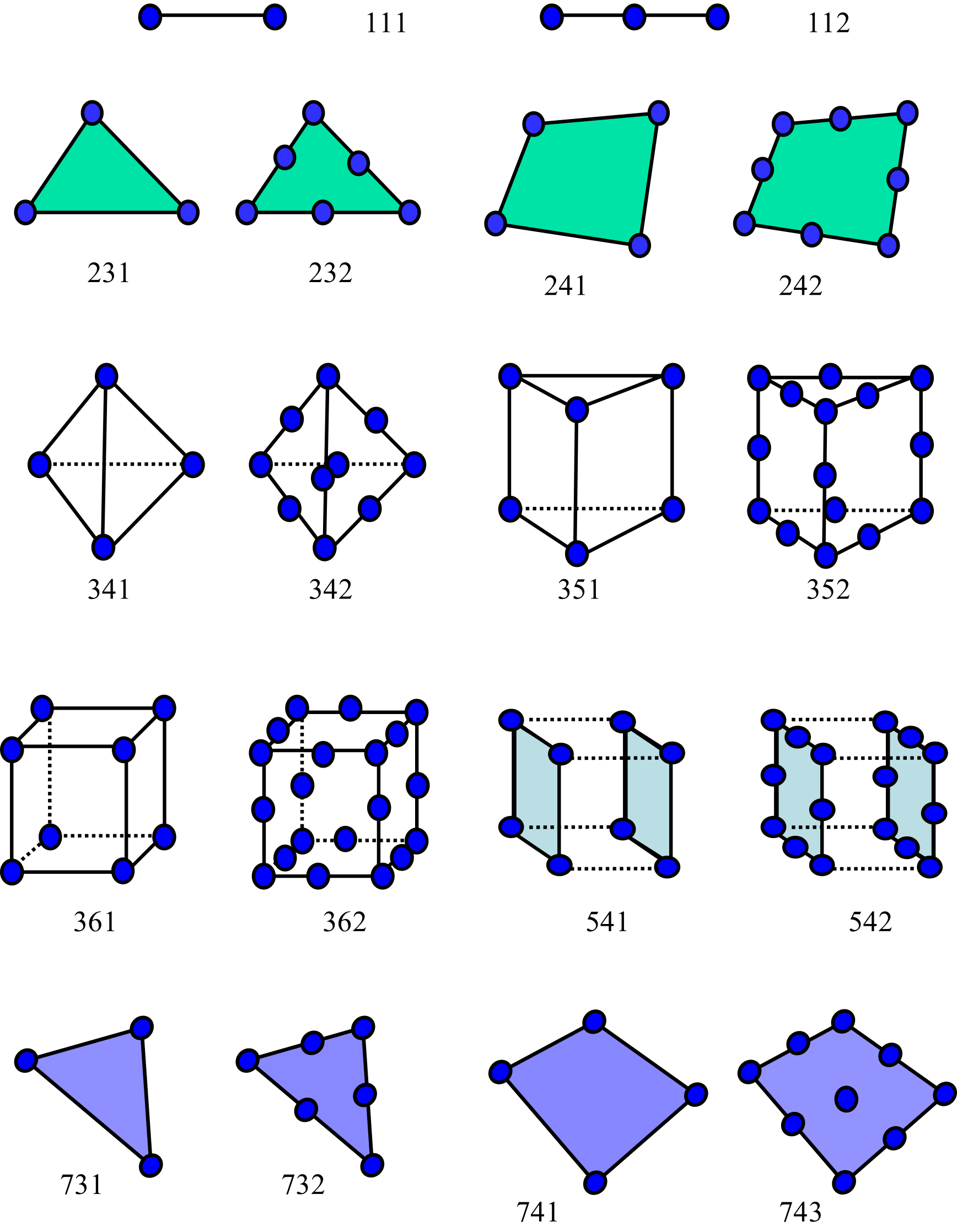
図 4.1.1 要素ライブラリ
(線要素)

(三角形平面要素)
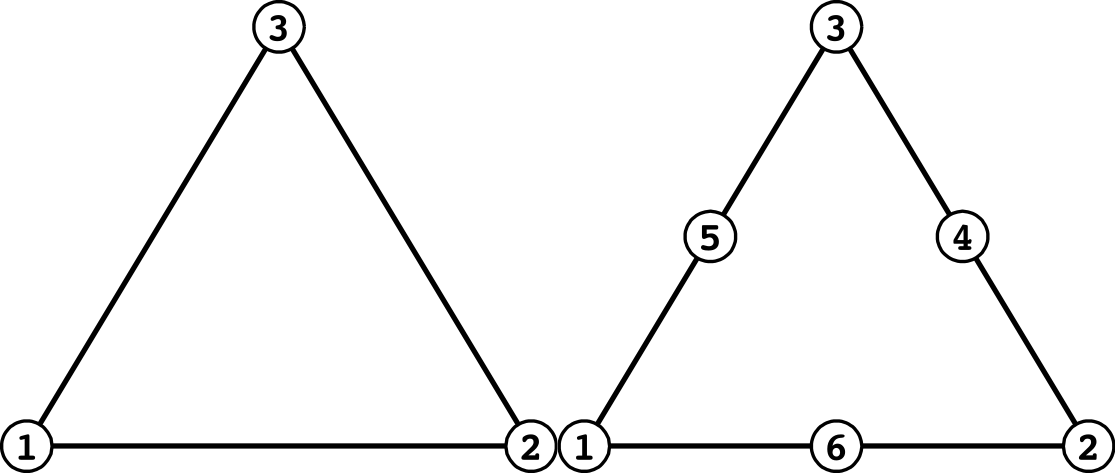
| 面番号 | 一次 | 二次 |
|---|---|---|
| 1 | 1 - 2 | 1 - 6 - 2 |
| 2 | 2 - 3 | 2 - 4 - 3 |
| 3 | 3 - 1 | 3 - 5 - 1 |
(四角形平面要素)
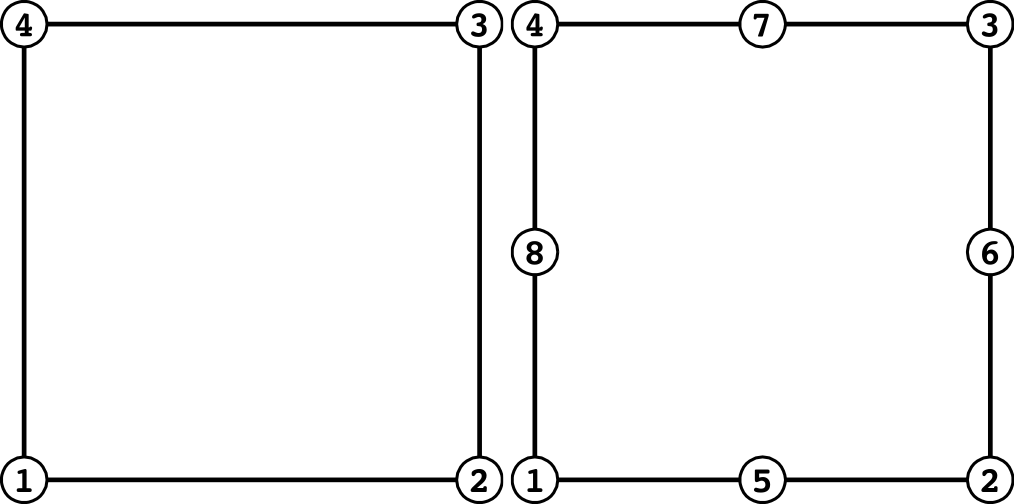
| 面番号 | 一次 | 二次 |
|---|---|---|
| 1 | 1 - 2 | 1 - 5 - 2 |
| 2 | 2 - 3 | 2 - 6 - 3 |
| 3 | 3 - 4 | 3 - 7 - 4 |
| 4 | 4 - 1 | 4 - 8 - 1 |
(四面体要素)
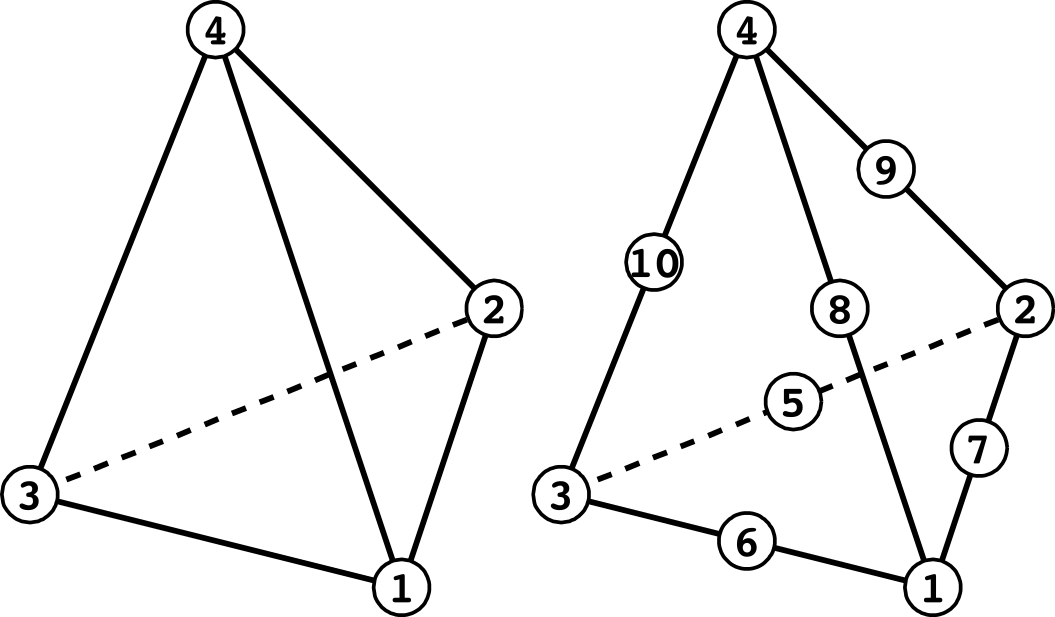
| 面番号 | 一次 | 二次 |
|---|---|---|
| 1 | 1 - 2 - 3 | 1 - 7 - 2 - 5 - 3 - 6 |
| 2 | 1 - 2 - 4 | 1 - 7 - 2 - 9 - 4 - 8 |
| 3 | 2 - 3 - 4 | 2 - 5 - 3 - 10 - 4 - 9 |
| 4 | 3 - 1 - 4 | 3 - 6 - 1 - 10 - 4 - 8 |
(五面体要素)
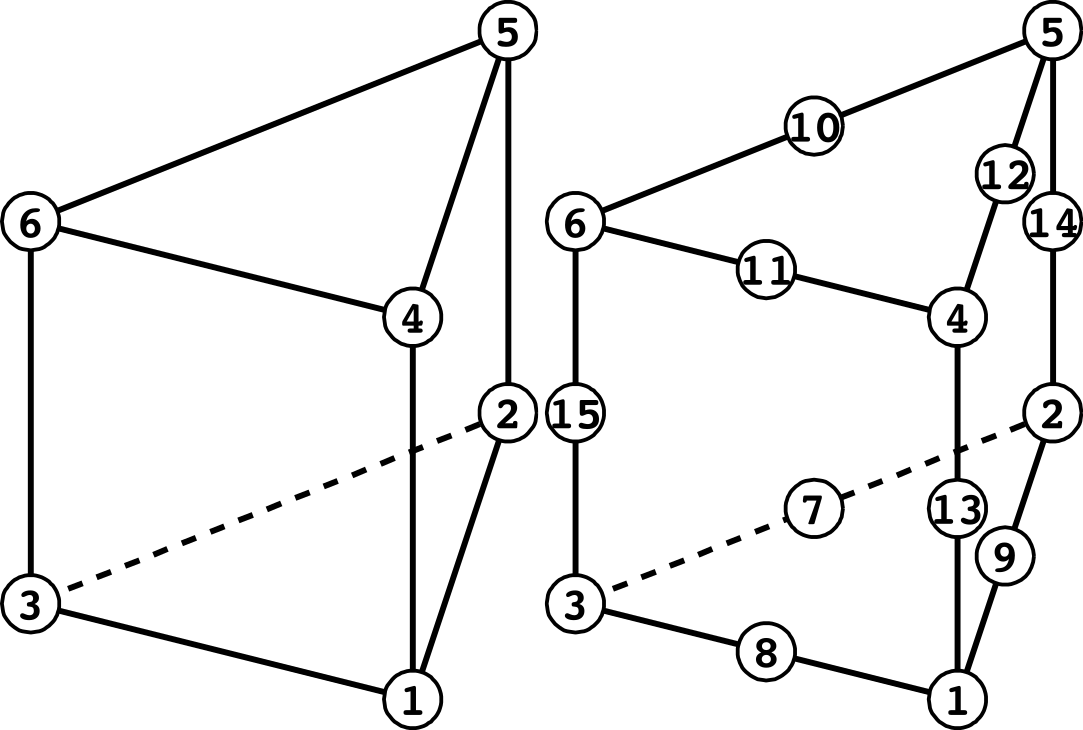
| 面番号 | 一次 | 二次 |
|---|---|---|
| 1 | 1 - 2 - 3 | 1 - 9 - 2 - 7 - 3 - 8 |
| 2 | 4 - 5 - 6 | 4 - 12 - 5 - 10 - 6 - 11 |
| 3 | 1 - 2 - 5 - 4 | 1 - 9 - 2 - 14 - 5 - 12 - 4 - 13 |
| 4 | 2 - 3 - 6 - 5 | 2 - 7 - 3 - 15 - 6 - 10 - 5 - 14 |
| 5 | 3 - 1 - 4 - 6 | 3 - 8 - 1 - 13 - 4 - 11 - 6 - 15 |
(六面体要素)
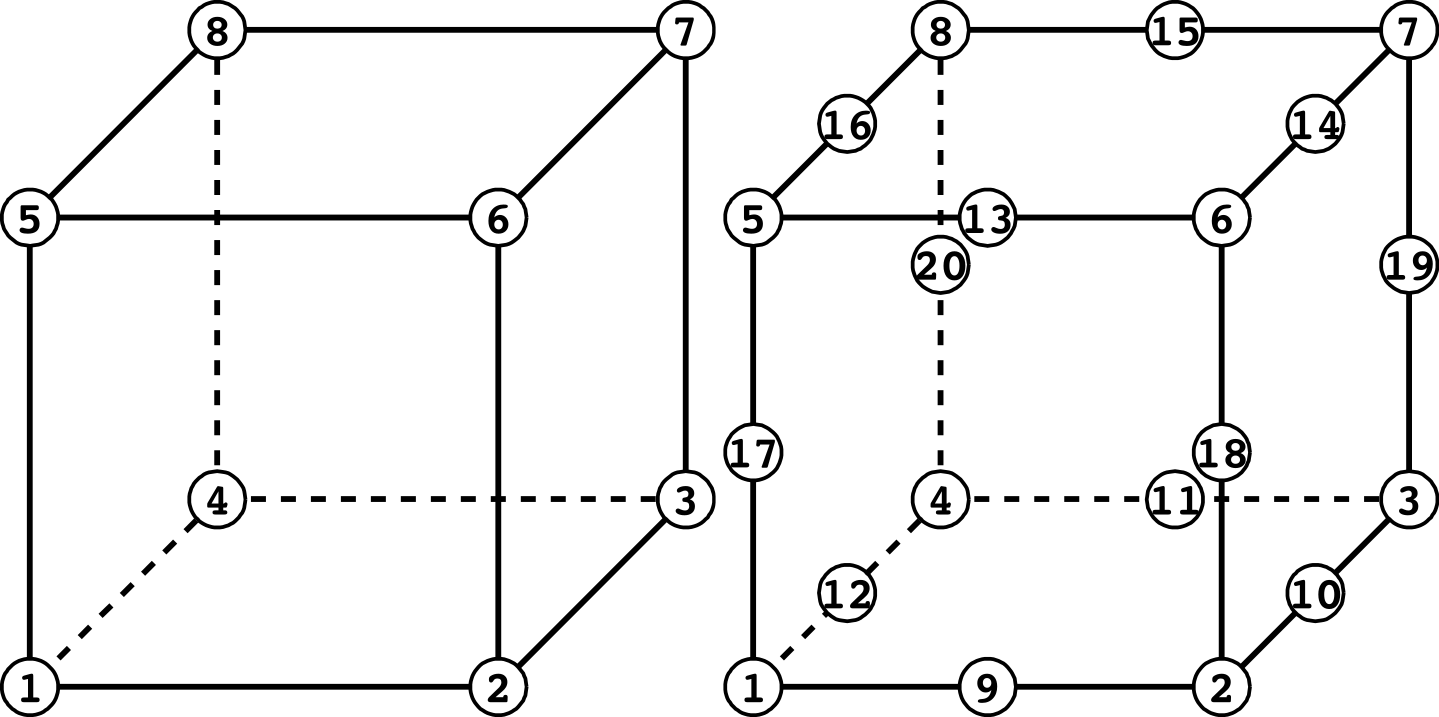
| 面番号 | 一次 | 二次 |
|---|---|---|
| 1 | 1 - 2 - 3 - 4 | 1 - 9 - 2 - 10 - 3 - 11 - 4 - 12 |
| 2 | 5 - 6 - 7 - 8 | 5 - 13 - 6 - 14 - 7 - 15 - 8 - 16 |
| 3 | 1 - 2 - 6 - 5 | 1 - 9 - 2 - 18 - 6 - 13 - 5 - 17 |
| 4 | 2 - 3 - 7 - 6 | 2 - 10 - 3 - 19 - 7 - 14 - 6 - 18 |
| 5 | 3 - 4 - 8 - 7 | 3 - 11 - 4 - 20 - 8 - 15 - 7 - 19 |
| 6 | 4 - 1 - 5 - 8 | 4 - 12 - 1 - 17 - 5 - 16 - 8 - 20 |
(梁要素)

(3自由度節点による梁要素)

節点1, 2は並進自由度、節点3, 4は回転自由度
(三角形シェル要素)
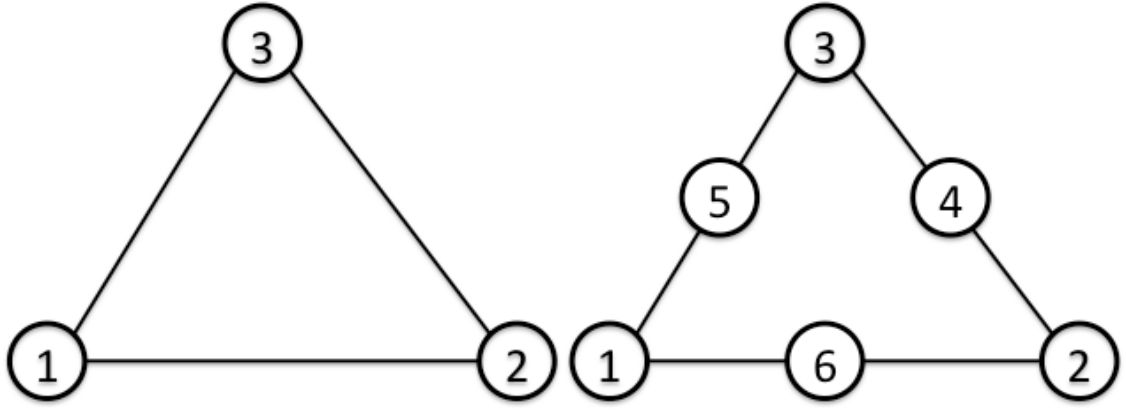
| Surface No. | Linear | Quadratic |
|---|---|---|
| 1 | 1 - 2 - 3 [front] | 1 - 6 - 2 - 4 - 3 - 5 [front] |
| 2 | 3 - 2 - 1 [back] | 3 - 4 - 2 - 6 - 1 - 5 [back] |
(3自由度節点による三角形シェル要素)
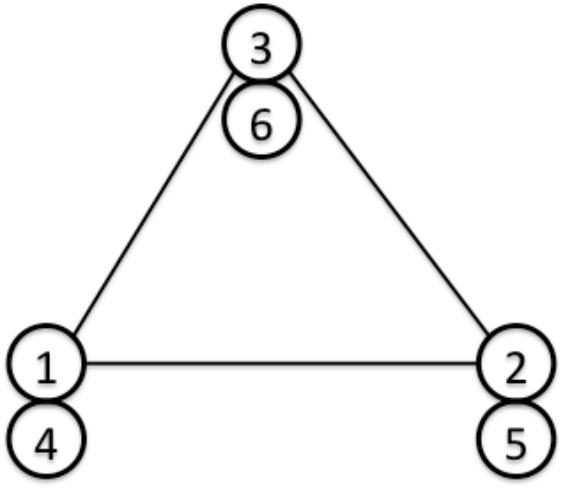
節点1, 2, 3は並進自由度、節点4, 5, 6は回転自由度
| Surface No. | Linear |
|---|---|
| 1 | 1 - 2 - 3 [front] |
| 2 | 3 - 2 - 1 [back] |
(四角形シェル要素)
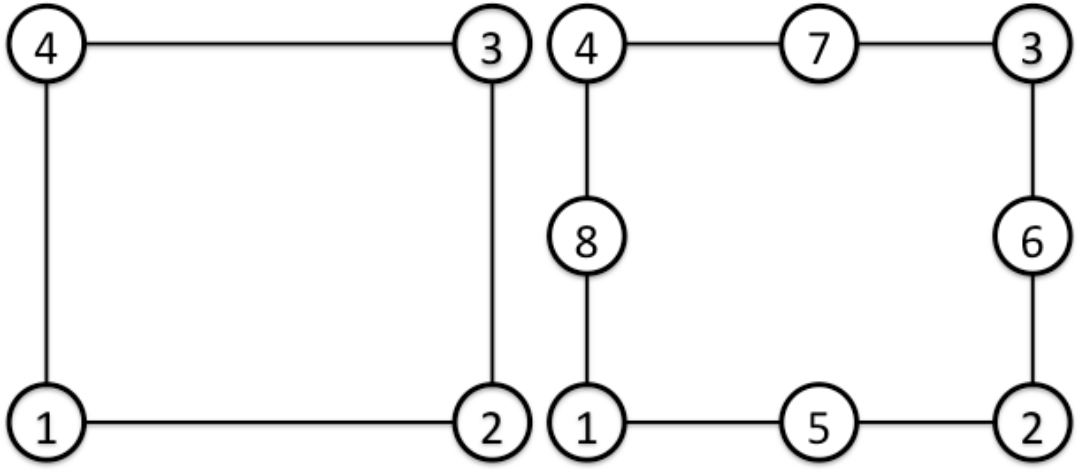
| Surface No. | Linear | Quadratic |
|---|---|---|
| 1 | 1 - 2 - 3 - 4 [front] | 1 - 5 - 2 - 6 - 3 - 7 - 4 - 8 [front] |
| 2 | 4 - 3 - 2 - 1 [back] | 4 - 7 - 3 - 6 - 2 - 5 - 1 - 8 [back] |
(3自由度節点による四角形シェル要素)
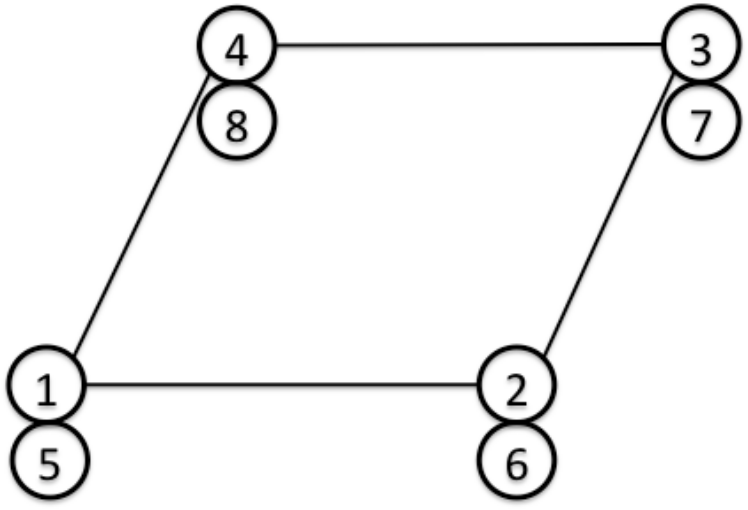
節点1, 2, 3, 4は並進自由度、節点5, 6, 7, 8は回転自由度
| Surface No. | Linear |
|---|---|
| 1 | 1 - 2 - 3 - 4 [front] |
| 2 | 4 - 3 - 2 - 1 [back] |
図 4.1.2 コネクティビティおよび面番号
材料データ
弾性静解析、線形動的解析および固有値解析
FrontISTRの弾性静解析および固有値解析では、等方性弾性材料を使用し、要素ごとにヤング率、ポアソン比、密度、線膨張係数を定義する必要がある。
これらの材料物性値はメッシュデータのヘッダー!SECTIONと!MATERIALにて定義する。以下にその例を示す。
#SECTIONの定義
!SECTION, TYPE=SOLID, EGRP=ALL, MATERIAL=M1
上記の!SECTION,では、ソリッドタイプの要素で、グループ名=ALLに所属する要素の、材料データ名をM1とすることを意味する。
次に材料データの定義方法を示す。
#材料名M1の材料では3種の物値を定義の意
!MATERIAL, NAME=M1, ITEM=3
#!ITEM=1ではヤング率とポアソン比を定義(必須)
!ITEM=1, SUBITEM=2
4000., 0.3
#!ITEM=2で質量密度を定義すること(ITEM=3のときには必須)
!ITEM=2
8.0102E-10
#!ITEM=3で線膨張係数を定義すること
!ITEM=3
1.0E-5
各ITEMの番号と物性種別が対応しており、ITEM番号さえ正しければ定義する順番は任意である。
ただし、ITEM=1内ではヤング率、ポアソン比の順に定義しなければならない。
熱伝導解析
FrontISTRの熱伝導解析では、温度依存性を考慮した等方性材料が使用できる。 定義する物性値はリンク、平面、ソリッドおよびシェル要素では、密度、比熱および熱伝導率を、インターフェース要素ではギャップ熱伝達係数とギャップ輻射係数である。 これらの物性値の定義方法の例を以下に示す。
リンク、平面およびソリッド要素の場合
!SECTIONと!MATERIALヘッダーにて定義する。
#セクションの定義
!SECTION, TYPE=SOLID, EGRP=ALL, MATERIAL=M1
上記の!SECTIONでは、ソリッドタイプの要素で、グループ名=ALLに所属する要素の、材料データ名をM1とすることを意味する。
以下、その材料データの定義方法である。
#材料名M1の材料では3種の物値を定義の意
!MATERIAL, NAME=M1, ITEM=3
#!ITEM=1では密度と温度を定義(必須)
!ITEM=1, SUBITEM=1
7850., 300.
7790., 500.
7700., 800.
#!ITEM=2では比熱と温度を定義(必須)
!ITEM=2
0.465, 300.
0.528, 500.
0.622, 800.
#!ITEM=3では熱伝導率と温度を定義(必須)
!ITEM=3
43., 300.
38.6, 500.
27.7, 800.
FrontISTRでは各ITEMの番号により物性の種類を識別しているので、両者の整合がとれていれば定義する順番は任意である。
インターフェース要素の場合
!SECTIONヘッダーで定義する。(材料データは不要)
#セクションの定義
!SECTION, TYPE=INTERFACE, EGRP=GAP
1.0, 20.15, 8.99835E-9, 8.99835E-9
上記の!SECTIONでは、インターフェース要素で、グループ名=GAPに所属する要素のギャップパラメータを定義している。
- 第1パラメータ: ギャップ幅
- 第2パラメータ: ギャップ熱伝達係数
- 第3パラメータ: ギャップ輻射係数1
- 第4パラメータ: ギャップ輻射係数2
シェル要素の場合
!SECTIONとMATERIALヘッダーで定義する。
#セクションの定義
!SECTION, TYPE=SHELL, EGRP=SH, MATERIAL=M2
10.0, 5
上記の!SECTIONでは、シェルタイプの要素で、グループ名=SHに所属する要素の、シェル特性を定義している。
- 第1パラメータ: シェル厚さ
- 第2パラメータ: 厚さ方向積分点数
また、同グループに所属する要素の材料物性を、材料データ名をM2とすることを意味する。
材料物性の定義方法は、等方性材料による単層シェルの場合は、ソリッド要素の場合と全く同様の指定方法が可能である。 ソリッド要素の説明を参照のこと。
これに加え、異方性材料や、積層シェルのために、以下に示す定義方法が可能である。
(例) 等方性材料 単層の場合
!MATERIAL, NAME=M1, ITEM=1
!ITEM=1,SUBITEM=4
0, 200000, 0.3, 2.0
- 第1パラメータ: 等方性0
- 第2パラメータ: ヤング率
- 第3パラメータ: ポアソン比
- 第4パラメータ: シェル厚さ
(例) 等方性材料 複層の場合(2層)
!MATERIAL, NAME=M1, ITEM=1
!ITEM=1,SUBITEM=7
0, 200000, 0.3, 2.0, 200000, 0.3, 2.0
- 第1パラメータ: 等方性0
- 第2パラメータ: ヤング率(第1層)
- 第3パラメータ: ポアソン比(第1層)
- 第4パラメータ: シェル厚さ(第1層)
- 第5パラメータ: ヤング率(第2層)
- 第6パラメータ: ポアソン比(第2層)
- 第7パラメータシェル厚さ(第2層)
積層数分の材料定数を入力することで,自動的に積層シェルを考慮した解析を行う.
シェルの総厚さは,自動的に各層の総和が入力される.積層順は,シェル法線方向,上から順に積層される.
(例) 異方性材料 単層の場合
!MATERIAL, NAME=M1, ITEM=1
!ITEM=1, SUBITEM=9
1, 28600., 0.15, 32.3 , 28600., 12434., 12434., 12434., 0.0
- 第1パラメータ: 異方性1
- 第2パラメータ: ヤング率E1
- 第3パラメータ: ポアソン比12
- 第4パラメータ: シェル厚さ
- 第5パラメータ: ヤング率E2
- 第6パラメータ: せん断係数G12
- 第7パラメータ: せん断係数G23
- 第8パラメータ: せん断係数G13
- 第9パラメータ: 異方性角度θ
異方性角度はθdegreeで指定する.
(例) 異方性材料 複層の場合(2層)
!MATERIAL, NAME=M1, ITEM=1
!ITEM=1, SUBITEM=17
1,28600.,0.15,32.3,28600.,12434.,12434.,12434.,0.0,28600.,0.15,32.3,(改行しない)
28600.,12434.,12434.,12434.,0.0
- 第1パラメータ: 異方性1
- 第2パラメータ: ヤング率E1(第1層)
- 第3パラメータ: ポアソン比12(第1層)
- 第4パラメータ: シェル厚さ(第1層)
- 第5パラメータ: ヤング率E2(第1層)
- 第6パラメータ: せん断係数G12(第1層)
- 第7パラメータ: せん断係数G23(第1層)
- 第8パラメータ: せん断係数G13(第1層)
- 第9パラメータ: 異方性角度θ(第1層)
- 第10パラメータ: ヤング率E1(第2層)
- 第11パラメータ: ポアソン比12(第2層)
- 第12パラメータ: シェル厚さ(第2層)
- 第13パラメータ: ヤング率E2(第2層)
- 第14パラメータ: せん断係数G12(第2層)
- 第15パラメータ: せん断係数G23(第2層)
- 第16パラメータ: せん断係数G13(第2層)
- 第17パラメータ: 異方性角度θ(第2層)
非線形静解析
FrontISTRの非線形静解析では、4.2.1に示した!SECTIONと!MATERIALにて定義する方法の他、解析制御データ中の!ELASTIC、!HYPERELASTIC、!PLASTICなども定義することができる。
以下にその例を示す。
(例) 超弾性材料の定義
!MATERIAL
#Neo Hooke超弾性材料の定義
!HYPERELASTIC, TYPE=NEOHOOKE
#C 10とDを定義(必須)
1000.0, 0.00005
(例) 弾塑性材料の定義
!MATERIAL
#等方性弾性材料の定義
!ELASTIC, TYPE=ISOTROPIC
#ヤング率とポアソン比を定義(必須)
21000.0, 0.3
#Drucker-Prager塑性材料の定義
!PLASTIC, TYPE=DRUCKER-PRAGER
#粘着力、摩擦角および硬化係数を定義(必須)
500.0, 4.0, 10.0