単純形状モデルによる検証

弾性静解析

本検証においては、片持ち梁を図9.1.1のようにメッシュ分割したものを対象とした。検証条件については図9.1.2に示す荷重条件を変えたexA～exGの7条件について解析を行った。なお、exGはexAと同じ荷重条件で、直接法ソルバーを使用した場合の検証ケースである。

表 9.1.1～表 9.1.7にケース別検証結果を示す。

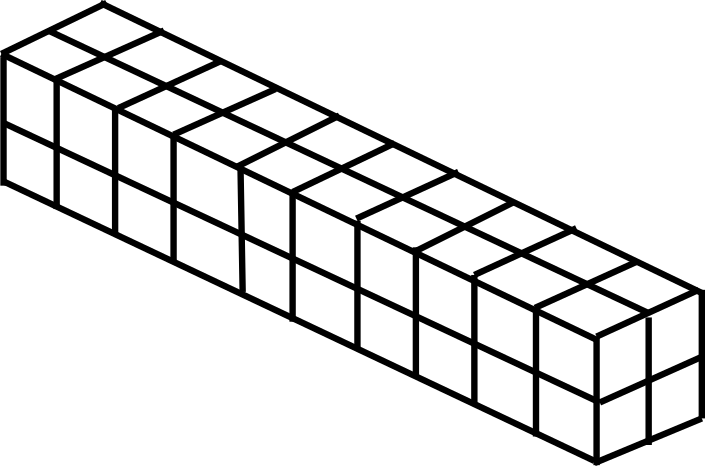図 9.1.1　片持ち梁のメッシュ分割例（六面体要素）


	(a) exA,G：集中荷重
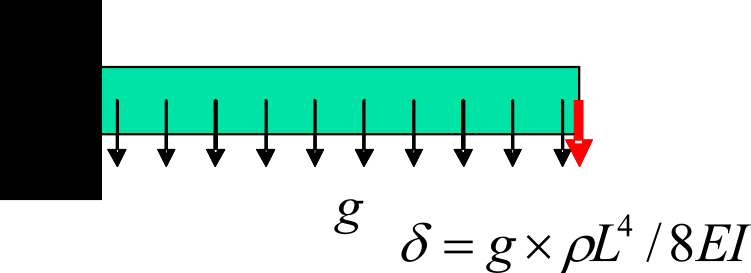	(b) exD：重力
	(c) exB：面分布荷重
	(d) exE：遠心力
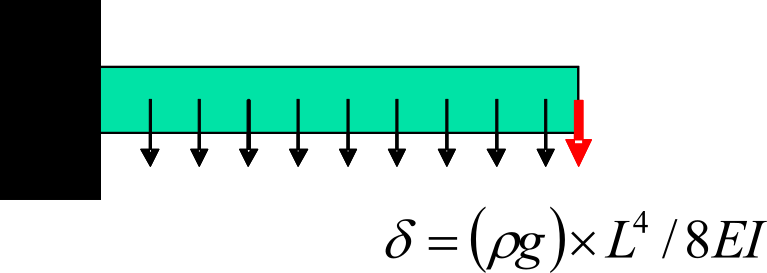	(e) exC：体積荷重
	(f) exF：熱荷重

項目	値
ヤング率	$E = 4000.0\ kgf/mm^2$
長さ	$L = 10.0\ mm$
ポアソン比	$\nu = 0.3$
断面積	$A = 1.0\ mm^2$
質量密度	$\rho = 8.0102 x 10^{-10}\ kg\,s^2/mm^4$
断面二次モーメント	$I = 1.0/12.0\ mm^4$
重力加速度	$g = 9800.0\ mm/s^2$
線熱膨張率	$\alpha = 1.0 \times 10^{-5}$

表 9.1.2 片持ち梁モデルの検証条件

表 9.1.1　exA：集中荷重問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= -1.000$		備考
		NASTRAN	ABAQUS	FrontISTR
A231	40	-0.338	-0.371	-0.371	33節点 / 平面応力状問題
A232	40	-0.942	-1.002	-1.002	105節点 / 平面応力状問題
A241	20	-0.720	-0.711	-0.711	33節点 / 平面応力状問題
A242	20	-0.910	-1.002	-1.002	85節点 / 平面応力状問題
A341	240	-0.384	-0.384	-0.386	99節点
A342	240	-0.990	-0.990	-0.999	525節点
A351	80	-0.353	-0.355	-0.351	99節点
A352	80	-0.993	-0.993	-0.992	381節点
A361	40	-0.954	-0.985	-0.984	99節点
A362	40	-0.994	-0.993	-0.993	220節点
A731	40	-	-	-0.991	33節点 / 直接法
A741	20	-	-	-0.996	33節点 / 直接法

表 9.1.2　exB：面分布荷重問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= -3.750$		備考
		NASTRAN	ABAQUS	FrontISTR
B231	40	-1.281	-1.403	-1.403	33節点 / 平面応力状問題
B232	40	-3.579	-3.763	-3.763	105節点 / 平面応力状問題
B241	20	-3.198	-2.680	-2.680	33節点 / 平面応力状問題
B242	20	-3.426	-3.765	-3.765	85節点 / 平面応力状問題
B341	240	-1.088	-1.449	-1.454	99節点
B342	240	-3.704	-3.704	-3.748	525節点
B351	80	-3.547	-1.338	-1.325	99節点
B352	80	-0.3717	-3.716	-3.713	381節点
B361	40	-3.557	-3.691	-3.688	99節点
B362	40	-3.726	-3.717	-3.717	220節点
B731	40	-	-	-3.722	33節点 / 直接法
B741	20	-	-	-3.743	33節点 / 直接法

表 9.1.3　exC：体積荷重問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= -2.944^{-5}$		備考
		NASTRAN	ABAQUS	FrontISTR
C231	40	-	-1.101e-5	-1.101e-5	33節点 / 平面応力状問題
C232	40	-	-2.951e-5	-2.951e-5	105節点 / 平面応力状問題
C241	20	-	-2.102e-5	-2.102e-5	33節点 / 平面応力状問題
C242	20	-	-2.953e-5	-2.953e-5	85節点 / 平面応力状問題
C341	240	-	-1.136e-5	-1.140e-5	99節点
C342	240	-	-2.905e-5	-2.937e-5	525節点
C351	80	-	-1.050e-5	-1.039e-5	99節点
C352	80	-	-2.914e-5	-2.911e-5	381節点
C361	40	-	-2.895e-5	-2.893e-5	99節点
C362	40	-	-2.915e-5	-2.915e-5	220節点
C731	40	-	-	-2.922e-5	33節点 / 直接法
C741	20	-	-	-2.938e-5	33節点 / 直接法

表 9.1.4　exD：重力問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= -2.944^{-5}$		備考
		NASTRAN	ABAQUS	FrontISTR
D231	40	-1.101e-5	-1.101e-5	-1.101e-5	33節点 / 平面応力状問題
D232	40	-2.805e-5	-2.951e-5	-2.951e-5	105節点 / 平面応力状問題
D241	20	-2.508e-5	-2.102e-5	-2.102e-5	33節点 / 平面応力状問題
D242	20	-2.684e-5	-2.953e-5	-2.953e-5	85節点 / 平面応力状問題
D341	240	-1.172e-5	-1.136e-5	-1.140e-5	99節点
D342	240	-2.906e-5	-2.905e-5	-2.937e-5	525節点
D351	80	-1.046e-5	-1.050e-5	-1.039e-5	99節点
D352	80	-2.917e-5	-2.914e-5	-2.911e-5	381節点
D361	40	-2.800e-5	-2.895e-5	-2.893e-5	99節点
D362	40	-2.919e-5	-2.915e-5	-2.915e-5	220節点
D731	40	-	-	-2.922e-5	33節点 / 直接法
D741	20	-	-	-2.938e-5	33節点 / 直接法

表 9.1.5　exE：遠心力問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= 2.635^{-3}$		備考
		NASTRAN	ABAQUS	FrontISTR
E231	40	2.410e-3	2.616e-3	2.650e-3	33節点 / 平面応力状問題
E232	40	2.447e-3	2.627e-3	2.628e-3	105節点 / 平面応力状問題
E241	20	2.386e-3	2.622e-3	2.624e-3	33節点 / 平面応力状問題
E242	20	2.387e-3	2.627e-3	2.629e-3	85節点 / 平面応力状問題
E341	240	2.708e-3	2.579e-3	2.625e-3	99節点
E342	240	2.639e-3	2.614e-3	2.638e-3	525節点
E351	80	2.642e-3	2.598e-3	2.625e-3	99節点
E352	80	2.664e-3	2.617e-3	2.616e-3	381節点
E361	40	2.611e-3	2.603e-3	2.603e-3	99節点
E362	40	2.623e-3	2.616e-3	2.616e-3	220節点
E731	40	-	-	2.619e-3	33節点 / 直接法
E741	20	-	-	2.622e-3	33節点 / 直接法

表 9.1.6　exF：熱応力荷重問題の検証結果

ケース名	要素数		予測値： $\delta_{max}= 1.000^{-2}$		備考
		NASTRAN	ABAQUS	FrontISTR
F231	40	-	1.016e-2	1.007e-2	33節点 / 平面応力状問題
F232	40	-	1.007e-2	1.007e-2	105節点 / 平面応力状問題
F241	20	-	1.010e-2	1.010e-2	33節点 / 平面応力状問題
F242	20	-	1.006e-2	1.006e-2	85節点 / 平面応力状問題
F341	240	-	1.047e-2	1.083e-2	99節点
F342	240	-	1.018e-2	1.022e-2	525節点
F351	80	-	1.031e-2	1.062e-2	99節点
F352	80	-	1.015e-2	1.017e-2	381節点
F361	40	-	1.026e-2	1.026e-2	99節点
F362	40	-	1.016e-2	1.016e-2	220節点

表 9.1.7　exG：直接法の検証結果（集中荷重問題）

ケース名	要素数		予測値：δmax= -1.000		備考
		NASTRAN	ABAQUS	FrontISTR
G231	40	-0.338	-0.371	-0.371	33節点 / 平面応力状問題
G232	40	-0.942	-1.002	-1.002	105節点 / 平面応力状問題
G241	20	-0.720	-0.711	-0.711	33節点 / 平面応力状問題
G242	20	-0.910	-1.002	-1.002	85節点 / 平面応力状問題
G341	240	-0.384	-0.384	-0.386	99節点
G342	240	-0.990	-0.990	-0.999	525節点
G351	80	-0.353	-0.355	-0.351	99節点
G352	80	-0.993	-0.993	-0.992	381節点
G361	40	-0.954	-0.985	-0.984	99節点
G362	40	-0.994	-0.993	-0.993	220節点
G731	40	-	-	-0.991	33節点 / 直接法
G741	20	-	-	-0.996	33節点 / 直接法

非線形静解析

(2-1) exnl1: 幾何学非線形解析

検証ケースexIの検証モデルは検証ケースexA～Gのモデルと同一のものである。図9.1.3に検証モデルの概念図を示す。このモデルについて幾何学的非線形解析を実施する。また、検証結果を表9.1.8に示す。

非線形計算は、最終荷重1.0Pに対して、荷重増分値0.1P，10ステップとする。

図 9.1.3　検証モデル

表 9.1.8　exI：検証結果（最大たわみ量履歴）

ケース名	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	線形解
I231	-	-	-	-	-	-	-	-	-	-	-
I232	-	-	-	-	-	-	-	-	-	-	-
I241	-	-	-	-	-	-	-	-	-	-	-
I242	-	-	-	-	-	-	-	-	-	-	-
I341	0.039	0.077	0.116	0.154	0.193	0.232	0.270	0.309	0.348	0.386	0.386
I342	0.099	0.200	0.300	0.400	0.499	0.599	0.698	0.797	0.896	0.995	0.999
I351	0.035	0.070	0.105	0.141	0.176	0.211	0.246	0.281	0.316	0.351	0.351
I352	0.099	0.198	0.298	0.397	0.496	0.595	0.693	0.792	0.890	0.987	0.992
I361	0.070	0.139	0.209	0.278	0.348	0.417	0.487	0.556	0.625	0.694	0.984
I362	0.099	0.197	0.298	0.397	0.496	0.595	0.694	0.793	0.891	0.988	0.993

(2-2) 　exnl2: 弾塑性変形解析

本検証問題はNational Agency for Finite Element Methods and Standards (U.K.): Test NL1 from NAFEMSを参考し、幾何学的非線形および複数の硬化則を取り入れ弾塑性変形解析を行った。図9.1.4に解析モデルを示す。

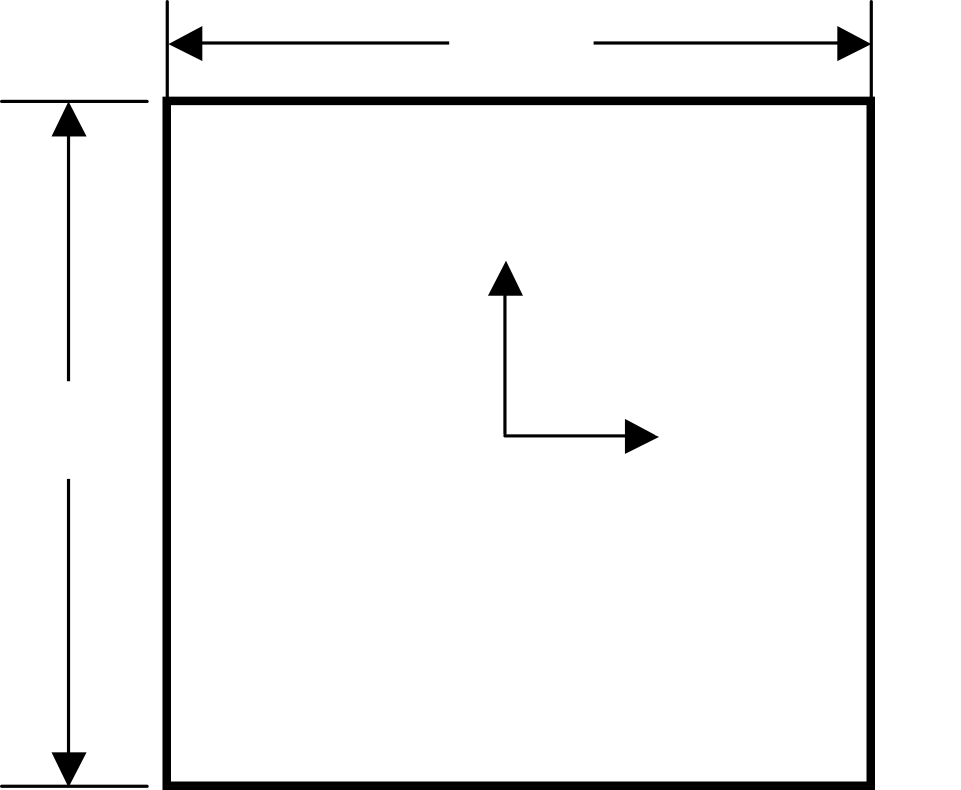
弾塑性変形解析モデル

図9.1.4　弾塑性変形解析モデル

（１）検証条件

項目	値
材料	Mises弾塑性材
ヤング率	$E = 250 GPa$
ポアソン比	$\nu=0.25$
初期降伏応力	$5 MPa$
初期降伏ひずみ	$0.25\times10^{-4}$
等方硬化係数	$H_i = 0$ または $62.5 GPa$

（２）境界条件

項目	境界条件	値
ステップ1	節点2と3に強制変位	$u_x = 0.2500031251 * 10^{-4}$
ステップ2	節点2と3に強制変位	$u_x = 0.25000937518 * 10^{-4}$
ステップ3	節点3と4に強制変位	$u_y = 0.2500031251 * 10^{-4}$
ステップ4	節点3と4に強制変位	$u_y = 0.25000937518 * 10^{-4}$
ステップ5	節点2と3に強制変位	$u_x = -0.25000937518 * 10^{-4}$
ステップ6	節点2と3に強制変位	$u_x = -0.2500031251 * 10^{-4}$
ステップ7	節点3と4に強制変位	$u_y = -0.25000937518 * 10^{-4}$
ステップ8	節点3と4に強制変位	$u_y = -0.2500031251 * 10^{-4}$

ここで示していない節点はすべて完全拘束される。この問題の理論解は以下のとおりである。

ひずみ ( $\times10^{-4}$ ) [ $\varepsilon_x$ , $\varepsilon_y$ , $\varepsilon_z$ ]	相当応力( $MPa$ ) [ $H_i=0\ H_k=0$ ; $H_i=62.5\ H_k=0$ ]
0.25, 0, 0	5.0; 5.0
0.50, 0, 0	5.0; 5.862
0.50, 0.25, 0	5.0; 5.482
0.50, 0.50, 0	5.0; 6.362
0.25, 0.50, 0	5.0; 6.640
0, 0.50, 0	5.0; 7.322
0, 0.25, 0	3.917; 4.230
0, 0, 0	5.0; 5.673

これに対して、計算結果は以下のとおりである。

ひずみ ( $\times10^{-4}$ ) [ $\varepsilon_x$ , $\varepsilon_y$ , $\varepsilon_z$ ]	相当応力( $MPa$ [ $H_i=0\ H_k=0$ ; $H_i=62.5\ H_k=0$ ])
$\varepsilon_{x}$	$\varepsilon_{y}$
0.25, 0, 0	5.0 (0.0%); 5.0 (0.0%)
0.50, 0, 0	5.0 (0.0%); 5.862 (0.0%)
0.50, 0.25, 0	5.0 (0.0%); 5.482 (0.0%)
0.50, 0.50, 0	5.0 (0.0%); 6.362 (-0.05%)
0.25, 0.50, 0	5.0 (0.0%); 6.640 (-0.21%)
0, 0.50, 0	5.0 (0.0%); 7.322 (-0.34%)
0, 0.25, 0	3.824 (-2.4%); 4.230 (-2.70%)
0, 0, 0	5.0 (0.0%); 5.673 (5.673 (-2.50%)

接触解析(1)

本検証問題はNational Agency for Finite Element Methods and Standards (U.K.):接触パーチテスト問題CGS-4を参考し、摩擦ありの有限すべり接触問題機能をテストするものである。図9.1.5に解析モデルを示す。

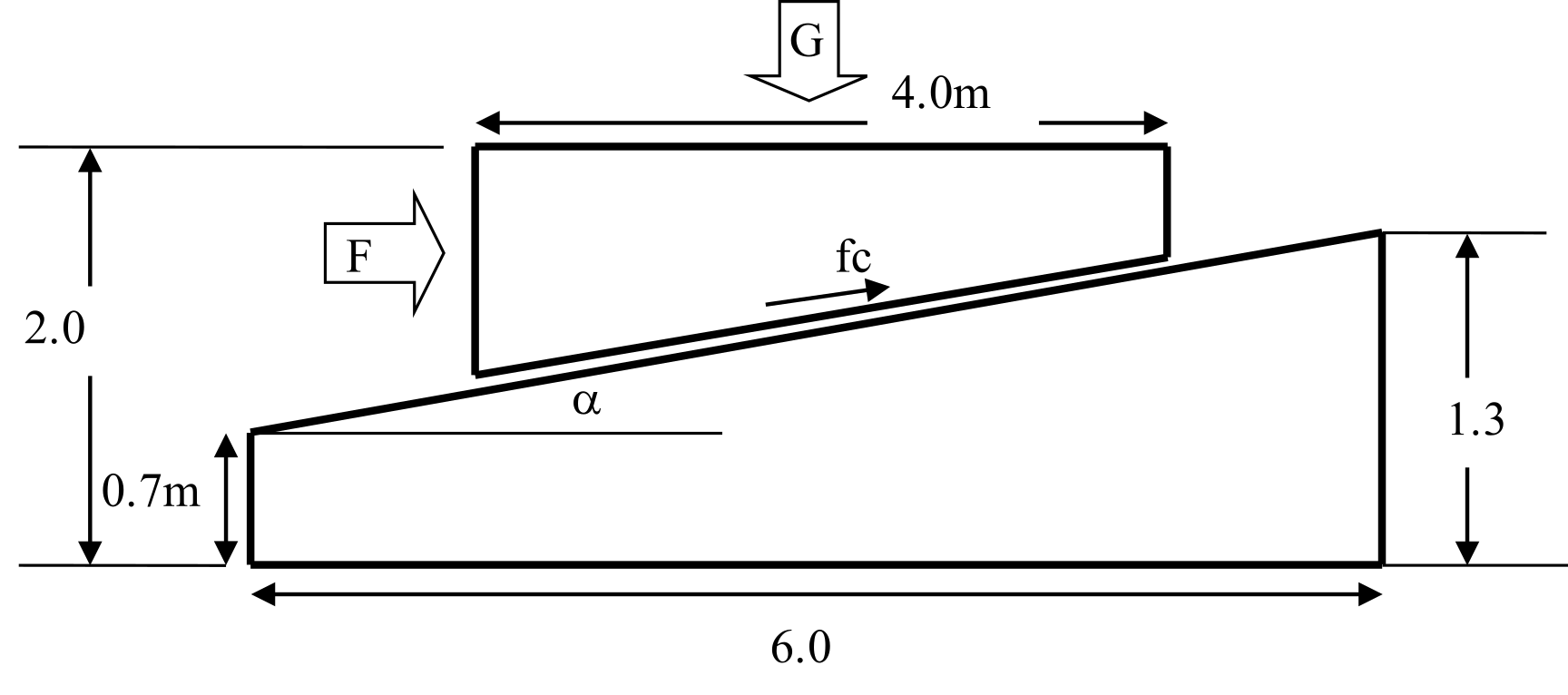
接触解析モデル

図9.1.5　接触解析モデル

この問題の釣り合い条件は以下のとおりである。

$Fcos\alpha - Gsin\alpha = \pm f_{c}$

粘着摩擦段階では摩擦力は $f_{c} = E_{t}\text{Δu}$ であり、すべり摩擦段階では $f_{c} = \mu(G \cos \alpha + F \sin \alpha)$ となる。

計算結果と解析解との比較は以下のとおりである。

$\mu$	$F/G$ 解析解	$F/G$ 計算結果
0.0	0.1	0.1
0.1	0.202	0.202
0.2	0.306	0.306
0.3	0.412	0.412

接触解析(2): ヘルツの接触問題

本検証では無限長さ円柱と無限平面のヘルツ接触問題を解析した。円柱の半径をR=8mmとし、変形体のヤング率E及びポアソンµ比はそれぞれ1100Mpaと0.0である。また、接触面積は円柱の半径と比べ十分小さいと仮定し、問題の対称性も考慮して、円柱の四分の一モデルにより解析を行った。

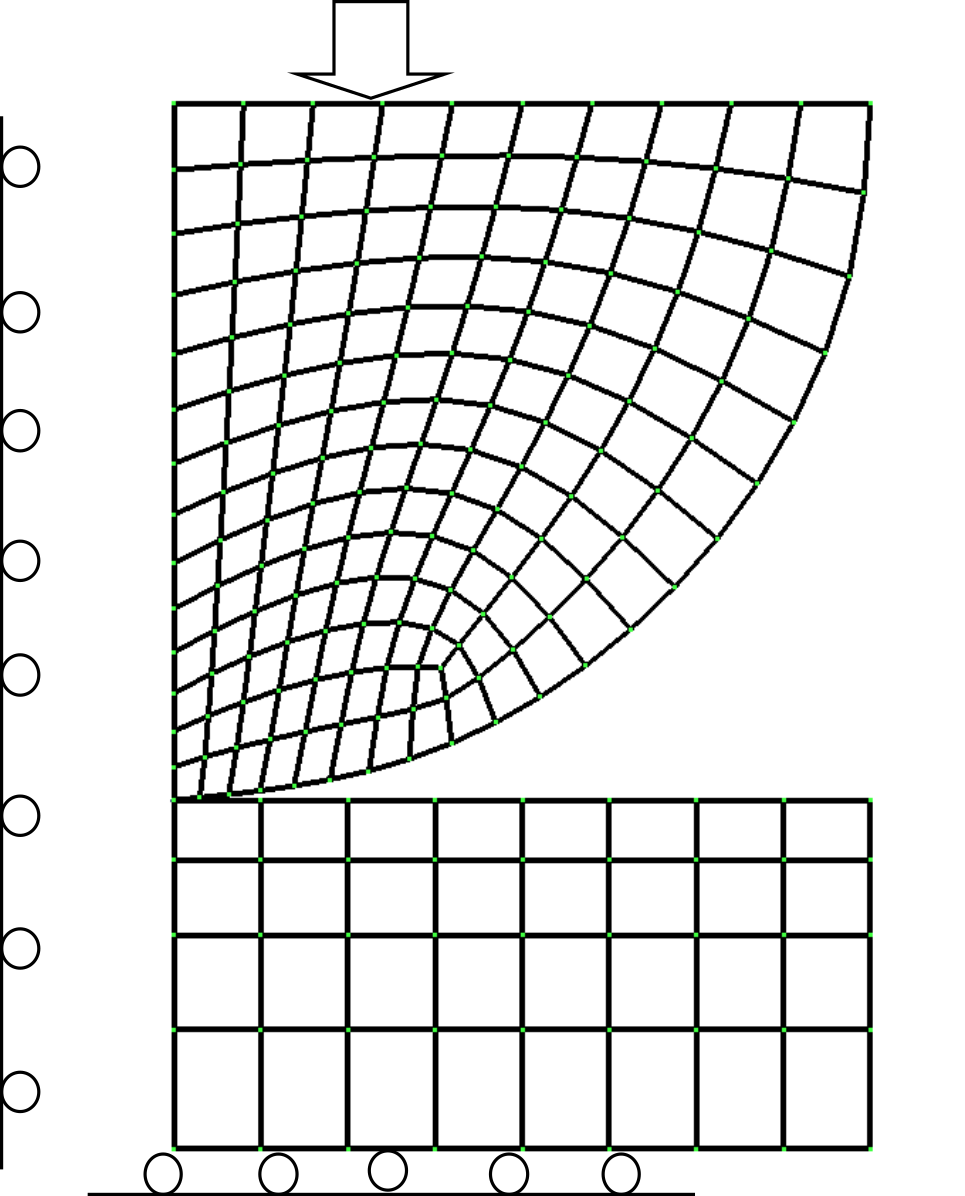図9.1.6　ヘルツ接触問題解析モデル

（1）接触半径の検証結果

接触半径を計算する理論式は以下のとおりである。

$a = \sqrt{\frac{4FR}{\pi E^{*}}}$

ここで、 $E^{*} = E/2(1 - \mu^{2})$ である。本計算では圧力 $F=100$ の時、接触半径 $a=1.36$ となる。

図9.1.7では接触点の等価節点力を示している。この節点力分布を外挿して、接触半径が得られる。

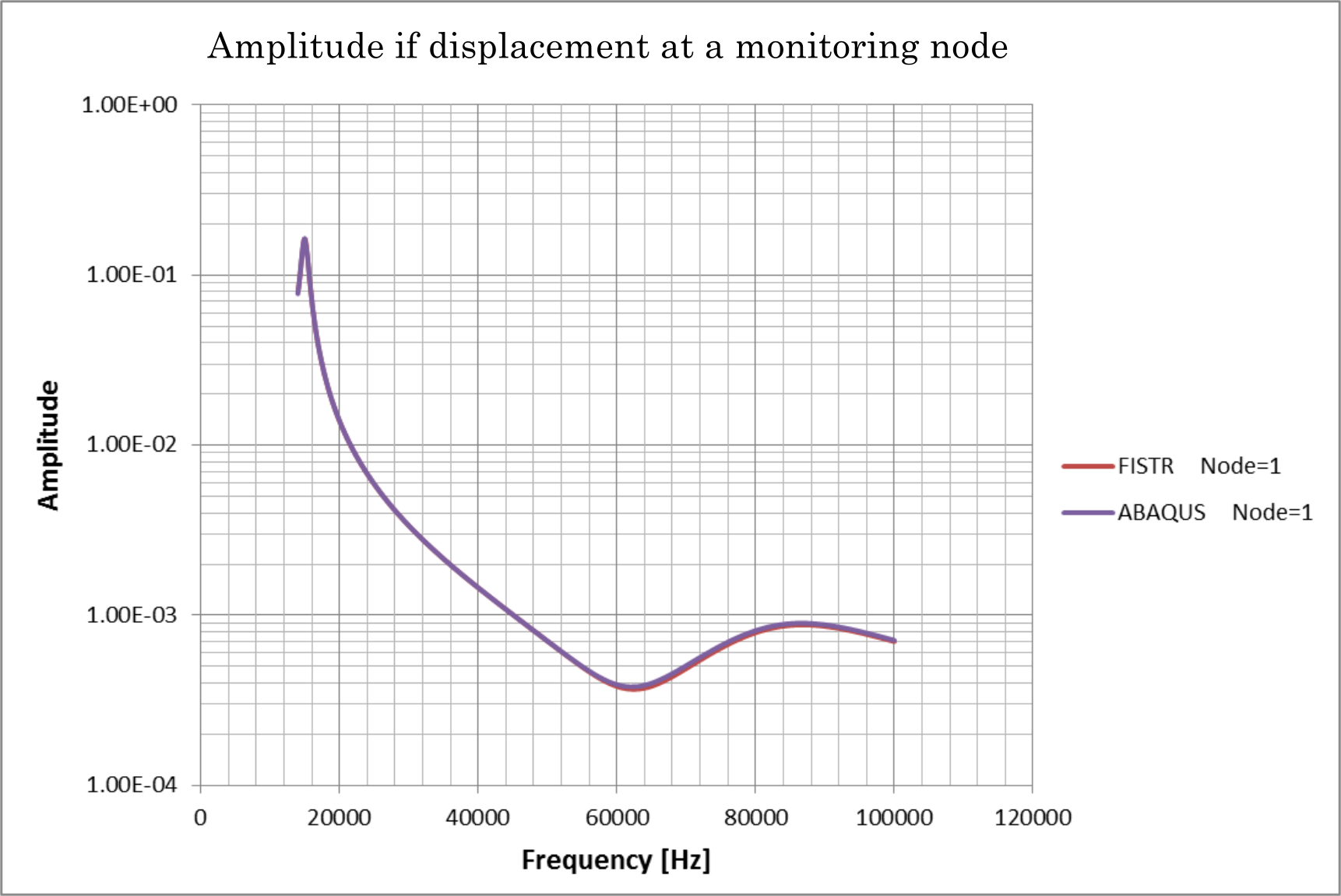
接触点の等価節点力分布

図9.1.7　接触点の等価節点力分布

（2）最大せん断応力の検証結果

理論解では、接触位置 $z = 0.78a$ において最大せん断応力が $\tau_{\max} = 0.30\sqrt{\frac{\text{FE}^{*}}{\pi R}}$ である。本計算条件では $\tau_{\max} = 14.2$ となる。これに対して、 $\tau_{\max} = 15.6$ の計算結果が得られた。

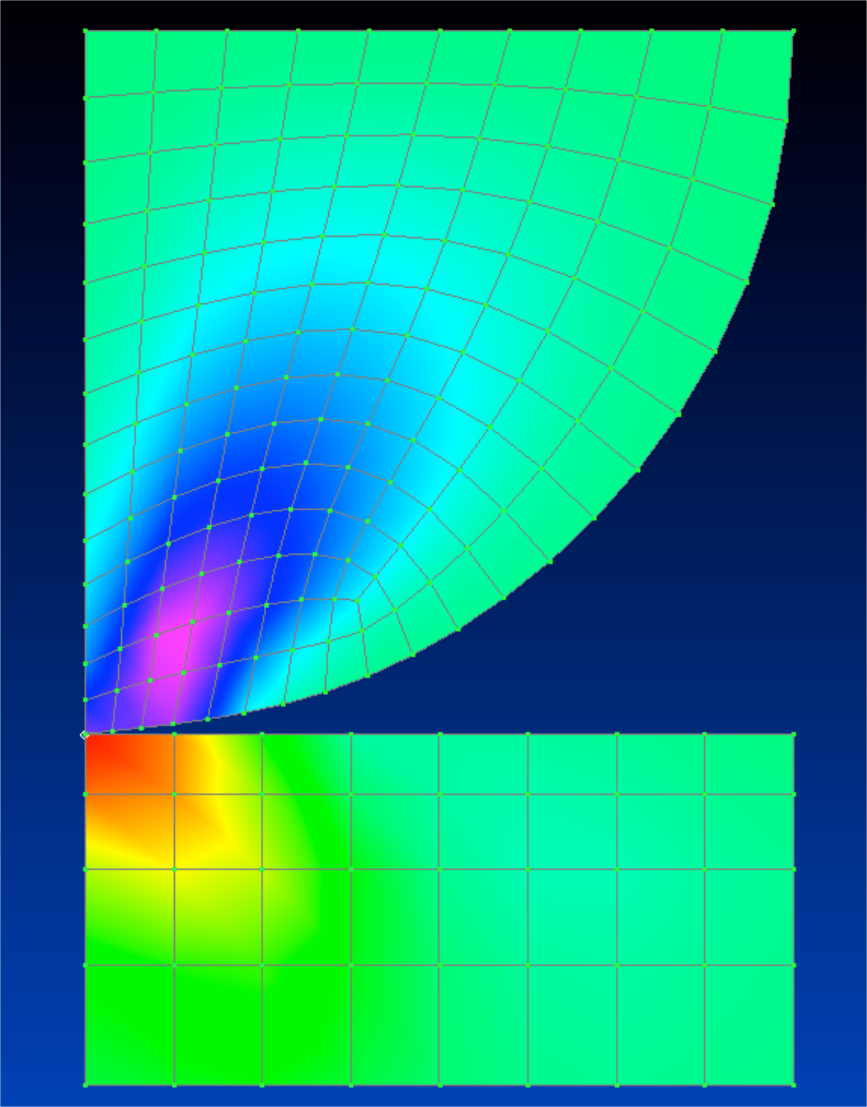図9.1.8　せん断応力分布（最大値=15.6）

(3) 固有値解析

検証ケースexJ～Kの検証モデルは検証ケースexA～Gのモデルと同一のものである。図9.1.9に検証モデルの概念図を示す。このモデルについて固有値解析を実施する。求める固有値は1次～3次固有値とする。なお、exJでは反復法ソルバーを、exKでは直接法ソルバーを使用するものとする。また、検証結果を表9.1.9～表 9.1.12に示す。

図 9.1.9　検証モデル

片持ち梁の振動固有値は次式で求まる。

第1次 $n_1 = \frac{1.875^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$ 第2次 $n_2 = \frac{4.694^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$ 第3次 $n_3 = \frac{7.855^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$

検証モデルの特性値は

項目	値
$I$	$10.0 mm$
$E$	$4000.0 kgf /mm^2$
$l$	$1.0/12.0 mm^4$
$\omega$	$7.85 * 10^{-6} kgf/mm^3$
$g$	$9800.0 mm/sec^2$

である。従って3次までの固有値は次のとおりである。

モード番号	値
$n_1$	3.609e3
$n_2$	2.262e4
$n_3$	6.335e4

表 9.1.9　exJ：反復法での検証結果（1次固有値）

ケース名	要素数	予測値：n1=3.609e3		備考
		NASTRAN	FrontISTR
J231	40	5.861e3	5.861e3	33節点 / 平面応力状問題
J232	40	3.596e3	3.593e3	105節点 / 平面応力状問題
J241	20	3.586e3	4.245e3	33節点 / 平面応力状問題
J242	20	3.590e3	3.587e3	85節点 / 平面応力状問題
J341	240	5.442e3	5.429e3	99節点
J342	240	3.621e3	3.595e3	525節点
J351	80	3.695e3	4.298e3	99節点
J352	80	3.610e3	3.609e3	381節点
J361	40	3.679e3	3.619e3	99節点
J362	40	3.611e3	3.606e3	220節点

表 9.1.10　exJ：反復法での検証結果（2次固有値）

ケース名	要素数	予測値：n2=2.262e4		備考
		NASTRAN	FrontISTR
J231	40	3.350e4	3.351e4	33節点 / 平面応力状問題
J232	40	2.163e4	2.156e4	105節点 / 平面応力状問題
J241	20	2.149e4	2.516e4	33節点 / 平面応力状問題
J242	20	2.149e4	2.143e4	85節点 / 平面応力状問題
J341	240	3.145e4	3.138e4	99節点
J342	240	2.171e4	2.155e4	525節点
J351	80	2.208e4	2.546e4	99節点
J352	80	2.156e4	2.149e4	381節点
J361	40	2.202e4	2.168e4	99節点
J362	40	2.154e4	2.144e4	220節点

注) 三次元モデルでは1次と2次が重根となるので、表中の2次の値には、3次の計算値を記述している。

表 9.1.11　exK：直接法での検証結果（1次固有値）

ケース名	要素数	予測値：n1=3.609e3		備考
		NASTRAN	FrontISTR
J231	40	5.861e3	5.861e3	33節点 / 平面応力状問題
J232	40	3.596e3	3.593e3	105節点 / 平面応力状問題
J241	20	3.586e3	4.245e3	33節点 / 平面応力状問題
J242	20	3.590e3	3.587e3	85節点 / 平面応力状問題
J341	240	5.442e3	5.429e3	99節点
J342	240	3.621e3	3.595e3	525節点
J351	80	3.695e3	4.298e3	99節点
J352	80	3.610e3	3.609e3	381節点
J361	40	3.679e3	3.619e3	99節点
J362	40	3.611e3	3.606e3	220節点
J731	40	-	3.606e3	220節点
J741	20	-	3.594e3	220節点

表 9.1.12　exK：直接法での検証結果（2次固有値）

ケース名	要素数	予測値：n2=2.262e4		備考
		NASTRAN	FrontISTR
J231	40	3.350e4	3.351e4	33節点 / 平面応力状問題
J232	40	2.163e4	2.156e4	105節点 / 平面応力状問題
J241	20	2.149e4	2.516e4	33節点 / 平面応力状問題
J242	20	2.149e4	2.143e4	85節点 / 平面応力状問題
J341	240	3.145e4	3.138e4	99節点
J342	240	2.171e4	2.155e4	525節点
J351	80	2.208e4	2.546e4	99節点
J352	80	2.156e4	2.149e4	381節点
J361	40	2.202e4	2.168e4	99節点
J362	40	2.154e4	2.144e4	220節点
J731	40	-	2.156e4	220節点
J741	20	-	2.153e4	220節点

注) 三次元モデルでは1次と2次が重根となるので、表中の2次の値には、3次の計算値を記述している。

(4) 熱伝導解析

定常熱伝導解析の共通する条件を図9.1.10に示す。検証ケースexM～exTの個別の条件を図9.1.11に示す。メッシュ分割は、exAと同等のものを使用することとする。

表 9.1.13～表 9.1.20にケース別に検証結果である温度分布テーブルを示す。

熱伝導解析


AB間長さ	$L = 10.0m$
断面積	$A = 1.0 mm^2$

熱伝導率の温度依存性

熱伝導率 $\lambda(W/mK)$	温度 $(^\circ C)$
50.0	0.0
35.0	500.0
20.0	1000.0

図 9.1.10　定常熱伝導解析の検証条件


exM:線形材料
exN:規定温度問題
exO:集中熱流束問題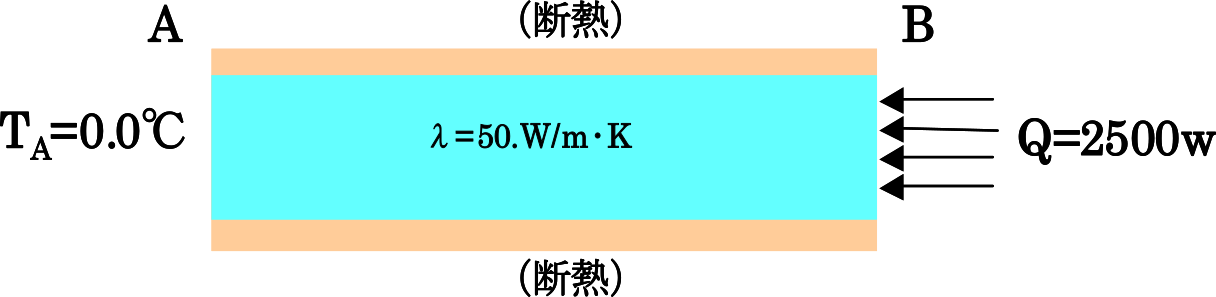
exP:分布熱流束問題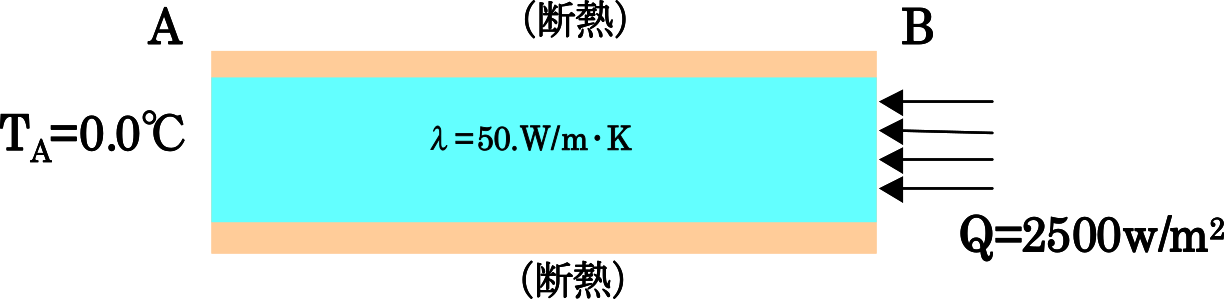
exQ:対流熱伝達問題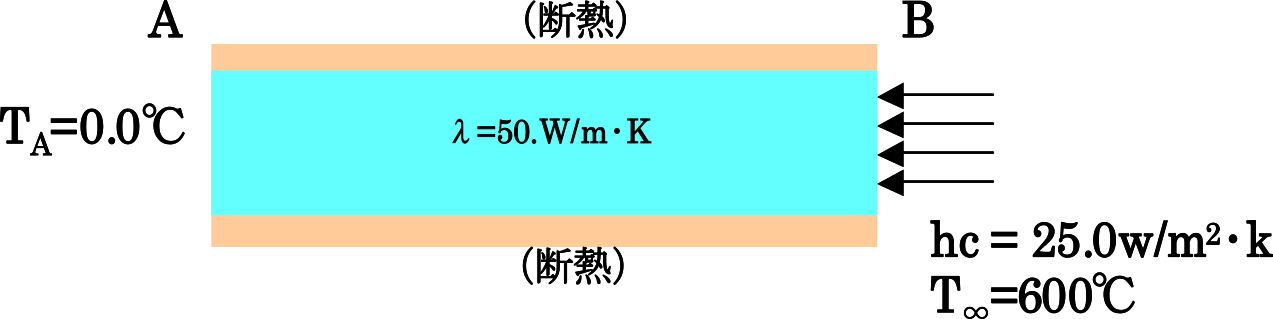
exR:輻射熱伝達問題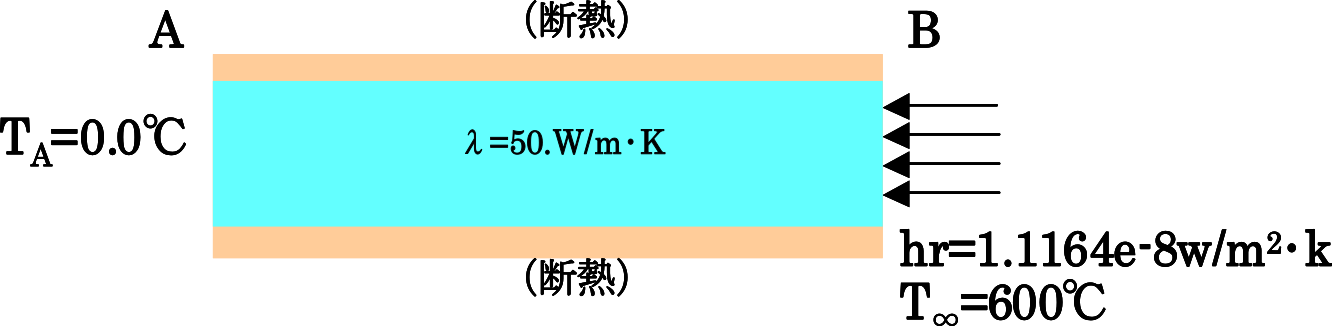
exS:体積発熱問題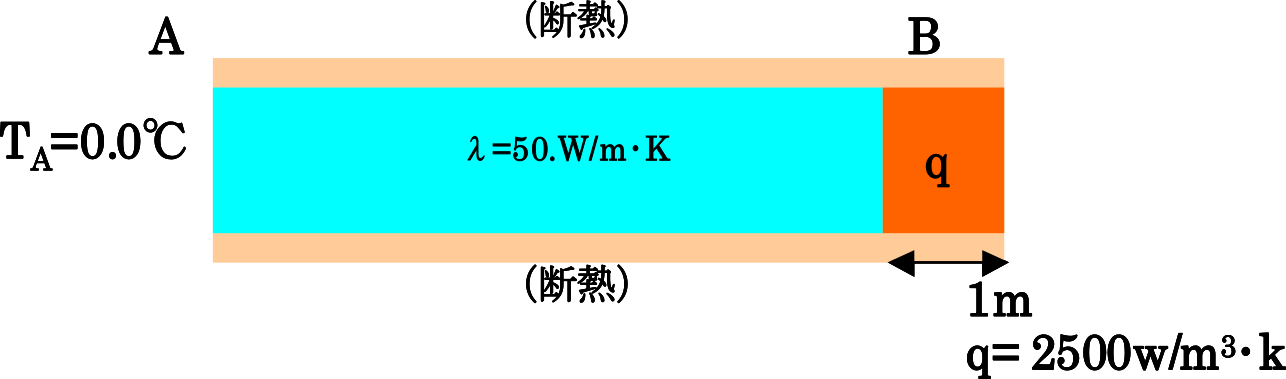
exT:内部ギャップ問題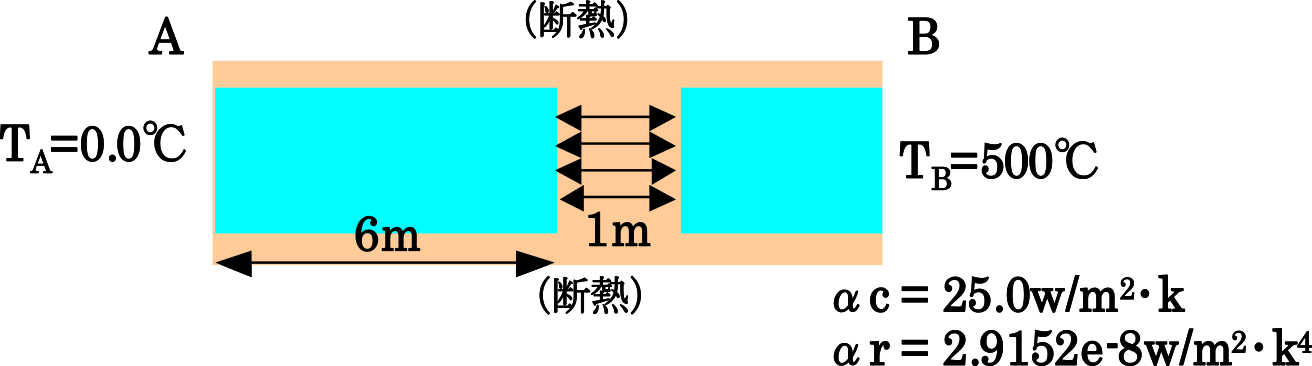

図 9.1.11　検証ケース別解析条件

表 9.1.13　exM：線形材料による定常計算の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
M361A	361	40／33	0.0	100.0	200.0	300.0	400.0	500.0
M361B	361	40／105	0.0	100.0	200.0	300.0	400.0	500.0
M361C	361	20／33	0.0	100.0	200.0	300.0	400.0	500.0
M361D	361	20／85	0.0	100.0	200.0	300.0	400.0	500.0
M361E	361	240／99	0.0	100.0	200.0	300.0	400.0	500.0
M361F	361	24／525	0.0	100.0	200.0	300.0	400.0	500.0
M361G	361	80／99	0.0	100.0	200.0	300.0	400.0	500.0

表 9.1.14　exN：規定温度問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	87.3	179.7	278.2	384.3	500.0
N231	231	40／33	0.0	87.2	179.5	278.0	384.1	500.0
N232	232	40／105	0.0	86.0	178.3	276.8	382.9	500.0
N241	241	20／33	0.0	87.3	179.7	278.2	384.3	500.0
N242	242	20／85	0.0	87.3	179.7	278.2	384.3	500.0
N341	341	240／99	0.0	87.3	179.7	278.2	384.3	500.0
N342	342	24／525	0.0	87.9	179.9	278.0	383.6	500.0
N351	351	80／99	0.0	87.3	179.7	278.2	384.3	500.0
N352	352	80／381	0.0	87.3	179.7	278.2	384.3	500.0
N361	361	40／99	0.0	87.3	179.7	278.2	384.3	500.0
N362	362	40／330	0.0	87.3	179.7	278.2	384.3	500.0
N731	731	40／33	0.0	87.3	179.7	278.2	384.3	500.0
N741	741	20／33	0.0	87.3	179.7	278.2	384.3	500.0

表 9.1.15　exO：集中熱流束問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
O231	231	40／33	0.0	103.2	213.7	333.3	464.8	612.6
O232	232	40／105	0.0	103.2	213.7	333.3	464.8	612.6
O241	241	20／33	0.0	103.2	213.7	333.3	464.8	612.6
O242	242	20／85	0.0	103.2	213.7	333.4	465.2	618.0
O341	341	240／99	-	-	-	-	-	-
O342	342	24／525	0.0	104.4	214.9	334.7	466.3	614.6
O351	351	80／99	-	-	-	-	-	-
O352	352	80／381	0.0	103.2	213.7	333.3	465.0	624.2
O361	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
O362	362	40／330	0.0	103.2	213.7	333.4	465.5	623.5
O731	731	40／33	0.0	103.2	213.7	333.3	464.8	612.5
O741	741	20／33	0.0	103.2	213.7	333.3	464.8	612.6

表 9.1.16　exP：分布熱流束問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
P231	231	40／33	0.0	103.2	213.7	333.3	464.8	612.6
P232	232	40／105	0.0	103.2	213.7	333.3	464.8	612.6
P241	241	20／33	0.0	103.2	213.7	333.3	464.8	612.6
P242	242	20／85	0.0	103.2	213.7	333.3	464.8	612.6
P341	341	240／99	-	-	-	-	-	-
P342	342	24／525	0.0	103.2	213.7	333.3	464.8	612.6
P351	351	80／99	-	-	-	-	-	-
P352	352	80／381	0.0	103.2	213.7	333.3	464.8	612.6
P361	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
P362	362	40／330	0.0	103.2	213.7	333.4	465.5	612.6
P731	731	40／33	0.0	103.2	213.7	333.3	464.8	612.5
P741	741	20／33	0.0	103.2	213.7	333.3	464.8	612.6

表 9.1.17　exQ：対流熱伝達問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	89.2	183.8	284.8	393.9	513.2
Q231	231	40／33	0.0	89.2	183.8	284.8	393.9	513.2
Q232	232	40／105	0.0	89.2	183.8	284.8	393.9	513.2
Q241	241	20／33	0.0	89.2	183.8	284.8	393.9	513.2
Q242	242	20／85	0.0	89.2	183.8	284.8	393.9	513.2
Q341	341	240／99	-	-	-	-	-	-
Q342	342	24／525	0.0	89.2	183.8	284.8	393.9	513.2
Q351	351	80／99	-	-	-	-	-	-
Q352	352	80／381	0.0	89.2	183.8	284.8	393.9	513.2
Q361	361	40／99	0.0	89.2	183.8	284.8	393.9	513.2
Q362	362	40／330	0.0	89.2	183.8	284.8	393.9	513.2
Q731	731	40／33	0.0	89.2	183.8	284.8	393.9	513.2
Q741	741	20／33	0.0	89.2	183.8	284.8	393.9	513.2

表 9.1.18　exR：輻射熱伝達問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	89.5	184.4	285.8	395.3	515.2
R231	231	40／33	0.0	89.5	184.4	285.8	395.3	515.2
R232	232	40／105	0.0	89.5	184.4	285.8	395.3	515.2
R241	241	20／33	0.0	89.5	184.4	285.8	395.3	515.2
R242	242	20／85	0.0	89.5	184.4	285.8	395.3	515.2
R341	341	240／99	-	-	-	-	-	-
R342	342	24／525	0.0	89.5	184.4	285.8	395.3	515.2
R351	351	80／99	-	-	-	-	-	-
R352	352	80／381	0.0	89.5	184.4	285.8	395.3	515.2
R361	361	40／99	0.0	89.5	184.4	285.8	395.3	515.2
R362	362	40／330	0.0	89.5	184.4	285.8	395.3	515.2
R731	731	40／33	0.0	89.5	184.4	285.8	395.3	515.2
R741	741	20／33	0.0	89.5	184.4	285.8	395.3	515.2

表 9.1.19　exS：体積発熱問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
S231	231	40／33	0.0	103.2	213.7	333.3	464.8	612.6
S232	232	40／105	0.0	103.2	213.7	333.3	464.8	612.6
S241	241	20／33	0.0	103.2	213.7	333.3	464.8	612.6
S242	242	20／85	0.0	103.2	213.7	333.3	464.8	612.6
S341	341	240／99	-	-	-	-	-	-
S342	342	24／525	0.0	103.2	213.7	333.3	464.8	612.6
S351	351	80／99	-	-	-	-	-	-
S352	352	80／381	0.0	103.2	213.7	333.3	464.8	612.6
S361	361	40／99	0.0	103.2	213.7	333.3	464.8	612.6
S362	362	40／330	0.0	103.2	213.7	333.3	464.8	612.6
S731	731	40／33	0.0	103.2	213.7	333.3	464.8	612.6
S741	741	20／33	0.0	103.2	213.7	333.3	464.8	612.6

表 9.1.20　exT：内部ギャップ問題の検証結果

ケース名	要素タイプ	要素／節点数	A端からの距離（ｍ）
			A端	2.0	4.0	6.0	8,0	B端
ABAQUS	361	40／99	0.0	88.6	182.4	282.6	387.7	500.0
S231	231	40／33	0.0	88.6	182.4	282.6	387.7	500.0
S232	232	40／105	0.0	88.6	182.4	282.6	387.7	500.0
S241	241	20／33	0.0	88.6	182.4	282.6	387.7	500.0
S242	242	20／85	0.0	88.6	182.4	282.6	387.7	500.0
S341	341	240／99	-	-	-	-	-	-
S342	342	24／525	0.0	88.6	182.4	282.6	387.7	500.0
S351	351	80／99	-	-	-	-	-	-
S352	352	80／381	0.0	88.6	182.4	282.6	387.7	500.0
S361	361	40／99	0.0	88.6	182.4	282.6	387.7	500.0
S362	362	40／330	0.0	88.6	182.4	282.6	387.7	500.0
S731	731	40／33	0.0	88.6	182.4	282.6	387.7	500.0
S741	741	20／33	0.0	88.6	182.4	282.6	387.7	500.0

線形動解析

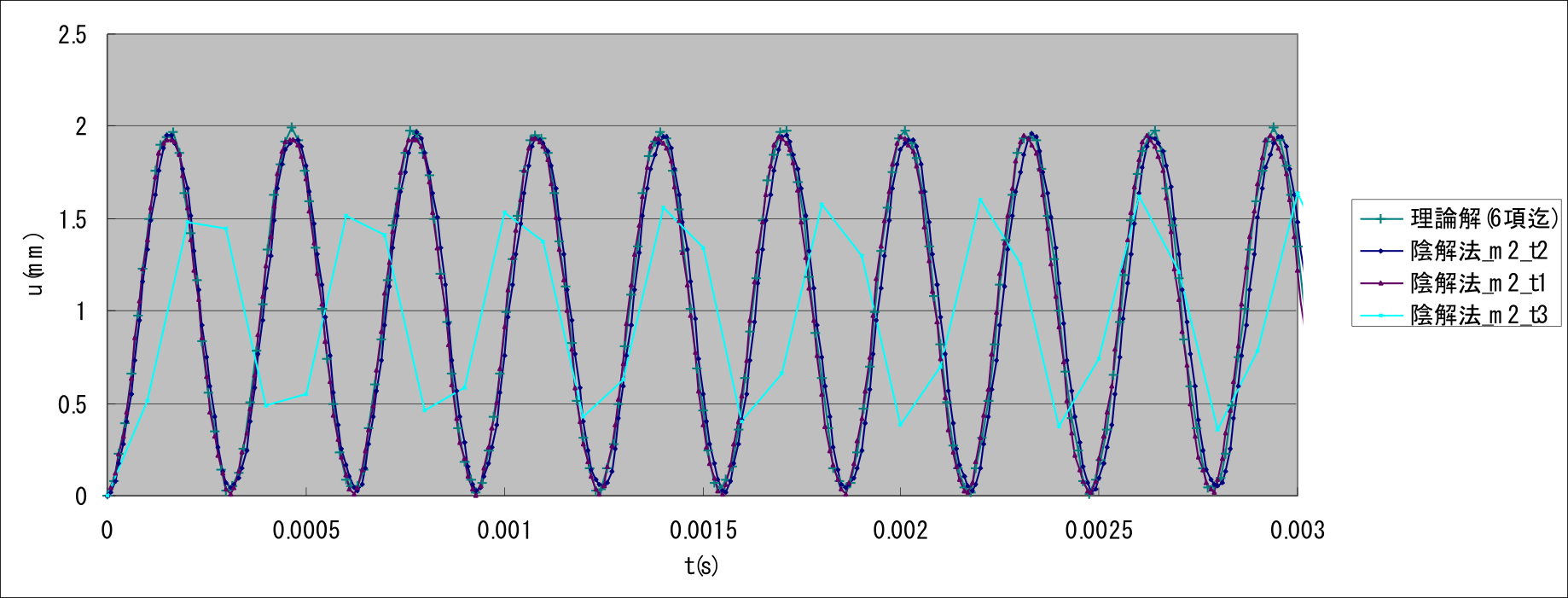
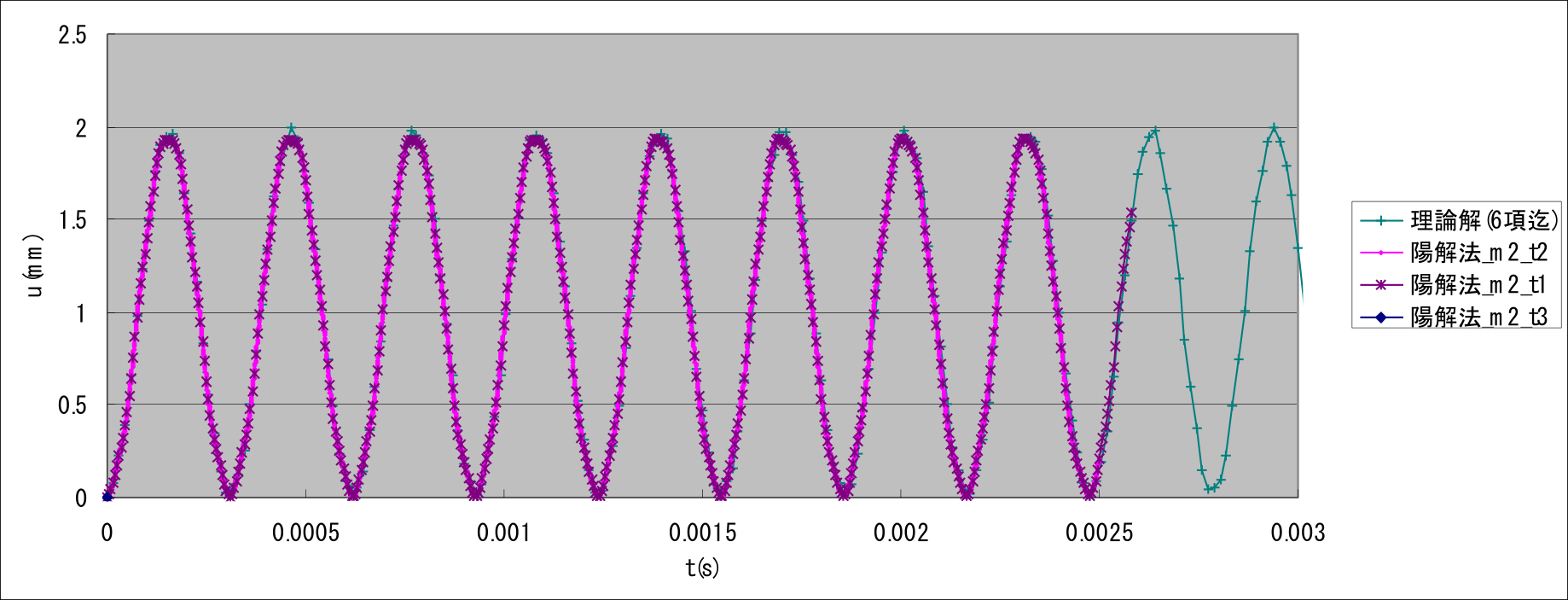
exWでは(1)項と同様の片持ち梁を対象に線形動解析を行った。図9.1.12に検証条件を示す。ここでは、同一のメッシュ分割に対して、時間増分が結果へ及ぼす影響を検証した。動的解析手法として、陰解法及び陽解法の両手法を使用し、要素タイプは361及び342を使用した。表9.1.22及び図 9.1.13～図 9.1.15に検証結果を示す。

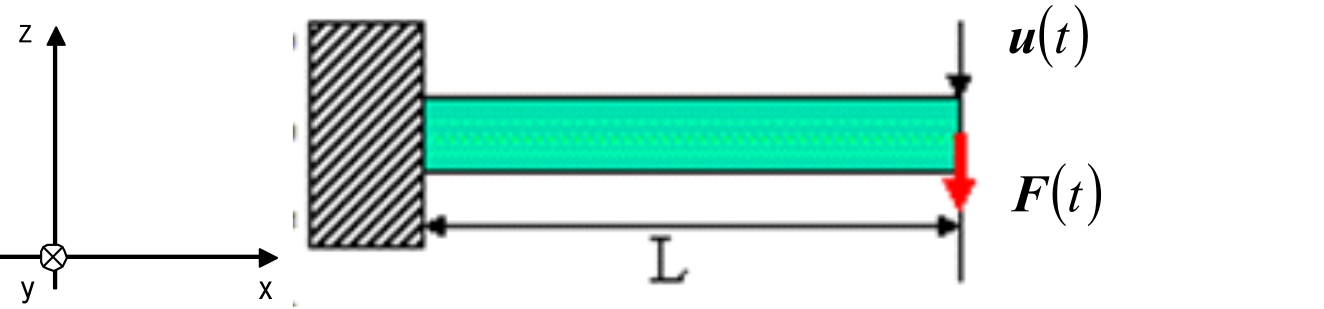
解析モデル

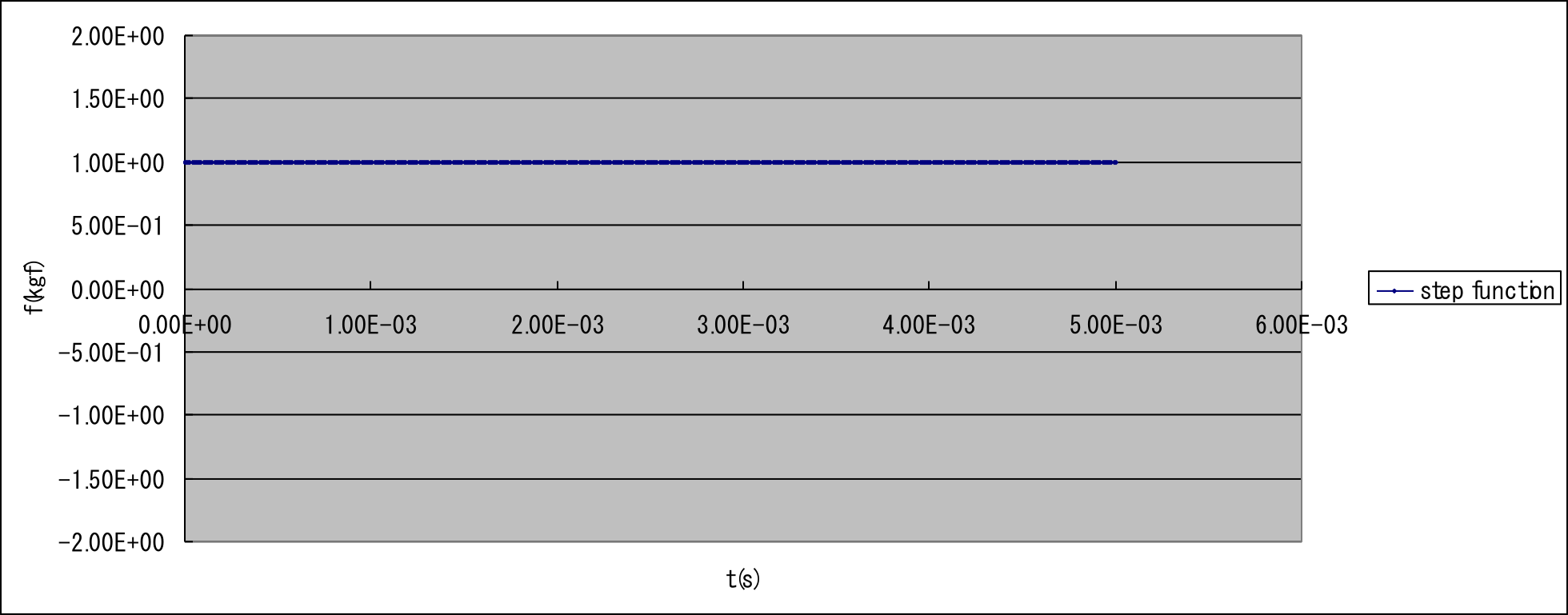
外力Fの時刻歴

加振点変位の理論解:

$F(t)=F_0 I(t)$

ここで、

$F_0:Constant\ vector$

$I(t)= \begin{cases} 0, t < 0 \\\ 1, 0 \leq t \end{cases}$

$u(t) = \frac{F_0 l^3}{EI} \sum^{\infty}_{i=1} \frac{1-\cos{\omega_i t}}{{\lambda_i}^4} \left\lbrace \cosh{\lambda_i}-\cos{\lambda_i}-\frac{\cosh{\lambda_i} + \cos{\lambda_i}}{\sin{\lambda_i}+\sin{\lambda_i}} (\sinh{\lambda_i} - \sin{\lambda_i}) \right\rbrace^2$

図 9.1.12　線形動解析の検証条件

検証条件:


長さ	$L$	$10.0\ mm$
断面幅	$a$	$1.0\ mm$
断面高さ	$b$	$1.0\ mm$
縦弾性係数	$E$	$4000.0\ kgf/mm^2$
ポアソン比	$\nu$	$0.3$
密度	$\rho$	$1.0E-09\ kgf\,s^2/mm^3$
重力加速度	$g$	$9800.0\ mm/s^2$
外力	$F_0$	$1.0\ kgf$


要素	6 面体 1 次要素
4 面体 2 次要素
解法	陰解法
Newmark- $\beta$ 法のパラメータ $\gamma$	1/2
Newmark- $\beta$ 法のパラメータ $\beta$	1/4
陽解法
減衰	無し

表 9.1.21　線形動解析の検証条件 (続き)

ケース名	要素タイプ	節点数	要素数	解法	時間増分 $\Delta t$ [sec]
W361_c0_im_m2_t1	361	99	40	陰解法	1.0E-06
W361_c0_im_m2_t2	361	99	40	陰解法	1.0E-05
W361_c0_im_m2_t3	361	99	40	陰解法	1.0E-04
W361_c0_ex_m2_t1	361	99	40	陰解法	1.0E-08
W361_c0_ex_m2_t2	361	99	40	陰解法	1.0E-07
W361_c0_ex_m2_t3	361	99	40	陰解法	1.0E-06
W342_c0_im_m2_t1	342	525	240	陽解法	1.0E-06
W342_c0_im_m2_t2	342	525	240	陽解法	1.0E-05
W342_c0_im_m2_t3	342	525	240	陽解法	1.0E-04
W342_c0_ex_m2_t1	342	525	240	陽解法	1.0E-08
W342_c0_ex_m2_t2	342	525	240	陽解法	5.0E-08
W342_c0_ex_m2_t3	342	525	240	陽解法	1.0E-07

表 9.1.22　exW：片持ち梁を対象とした線形動解析の検証結果

ケース名	要素タイプ	節点数	要素数	解法	時刻 t=0.002 sec におけるz方向変位 [mm]
W361_c0_im_m2_t1	361	99	40	陰解法	1.9753	1.9302
W361_c0_im_m2_t2	361	99	40	陰解法	1.9753	1.8686
W361_c0_im_m2_t3	361	99	40	陰解法	1.9753	0.3794
W361_c0_ex_m2_t1	361	99	40	陰解法	1.9753	1.9302
W361_c0_ex_m2_t2	361	99	40	陰解法	1.9753	1.9247
W361_c0_ex_m2_t3	361	99	40	陰解法	1.9753	発散
W342_c0_im_m2_t1	342	525	240	陽解法	1.9753	1.9431
W342_c0_im_m2_t2	342	525	240	陽解法	1.9753	1.8719
W342_c0_im_m2_t3	342	525	240	陽解法	1.9753	0.3873
W342_c0_ex_m2_t1	342	525	240	陽解法	1.9753	1.9359
W342_c0_ex_m2_t2	342	525	240	陽解法	1.9753	1.9358
W342_c0_ex_m2_t3	342	525	240	陽解法	1.9753	発散

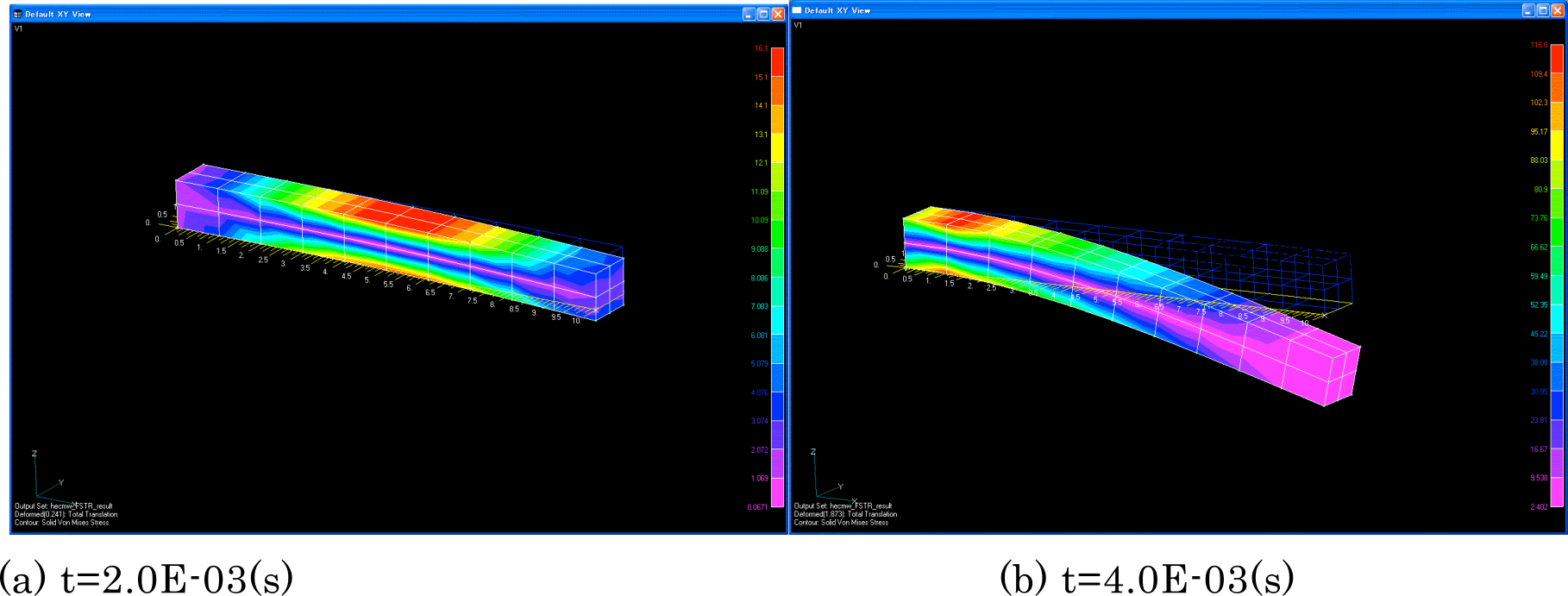
片もち梁の変形図及び相当応力分布

図 9.1.13　片もち梁の変形図及び相当応力分布

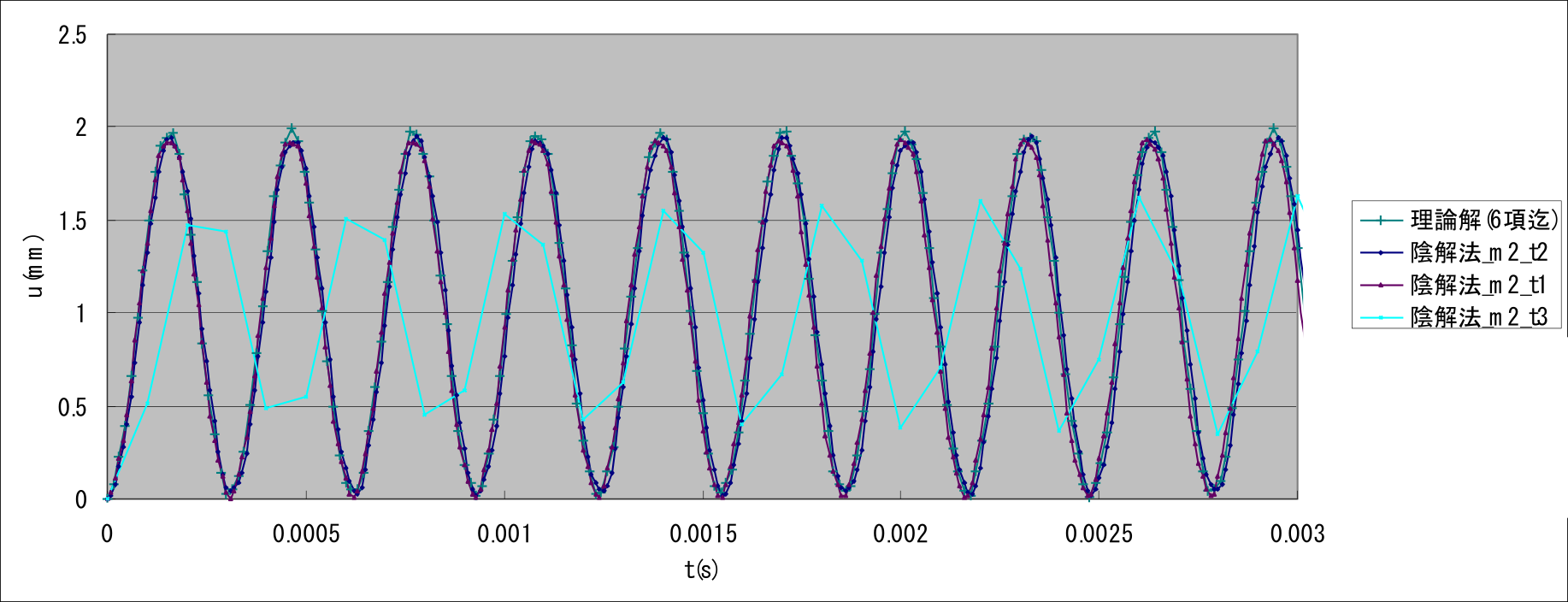
(a) 要素タイプ 361:陰解法

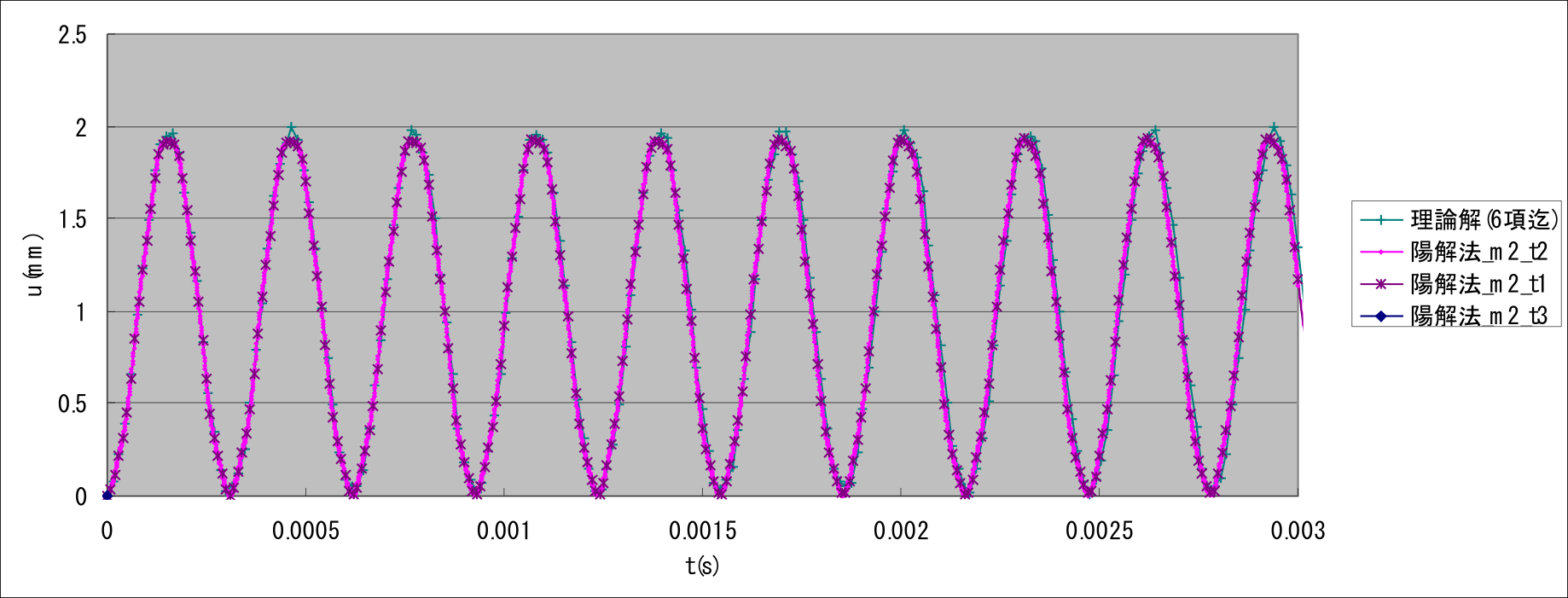
(b) 要素タイプ 361:陽解法

図9.1.14 加振点変位 $u_z$ の時刻歴

(a) 要素タイプ 342:陰解法

(b) 要素タイプ 342:陽解法

図 9.1.14　加振点変$u_z$位の時刻歴

周波数応答解析

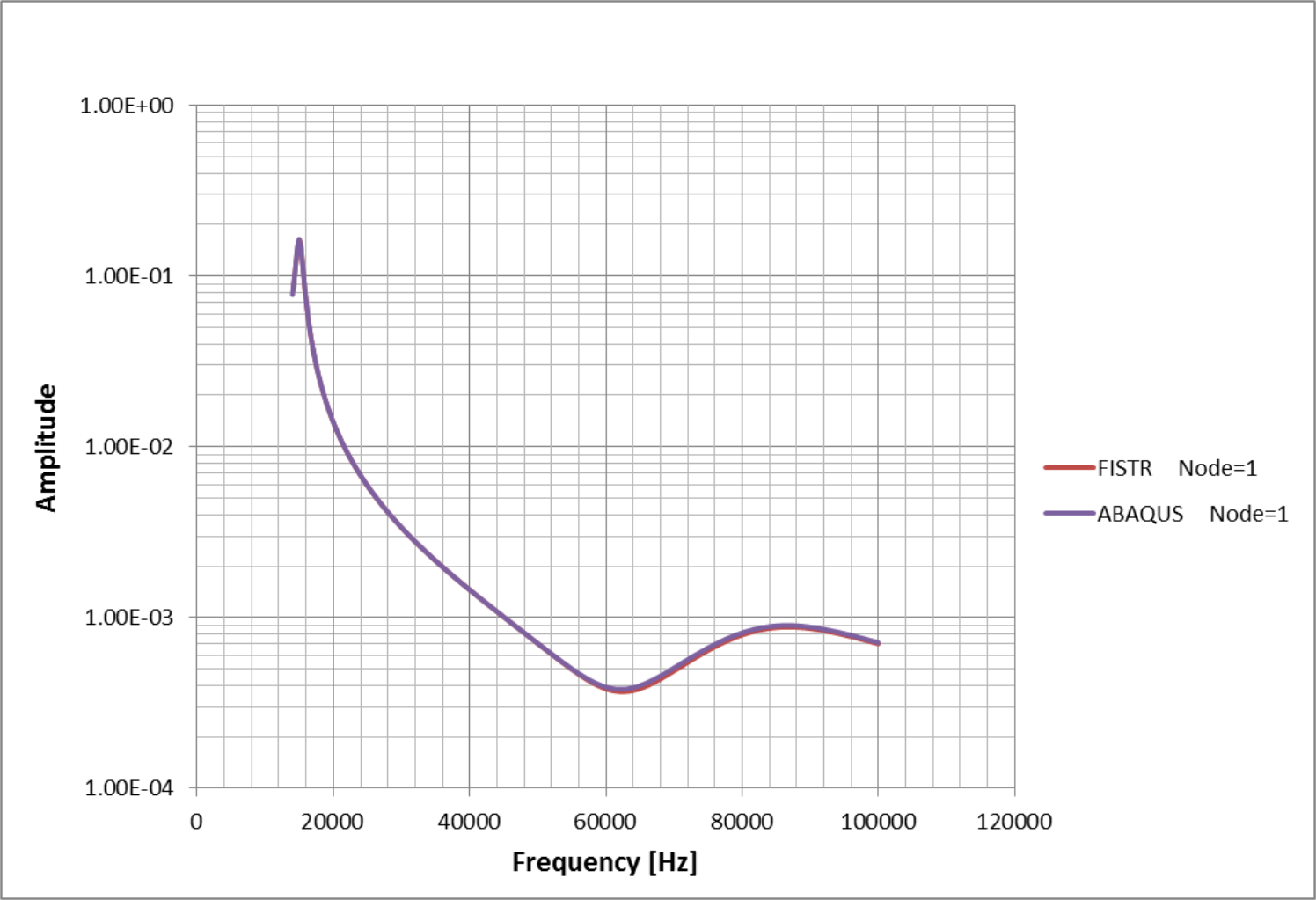
本検証では片持ち梁を対象に周波数応答解析を行い、汎用ソフトABAQUSの結果と比較することで検証を行った。解析モデル、検証条件を示す。

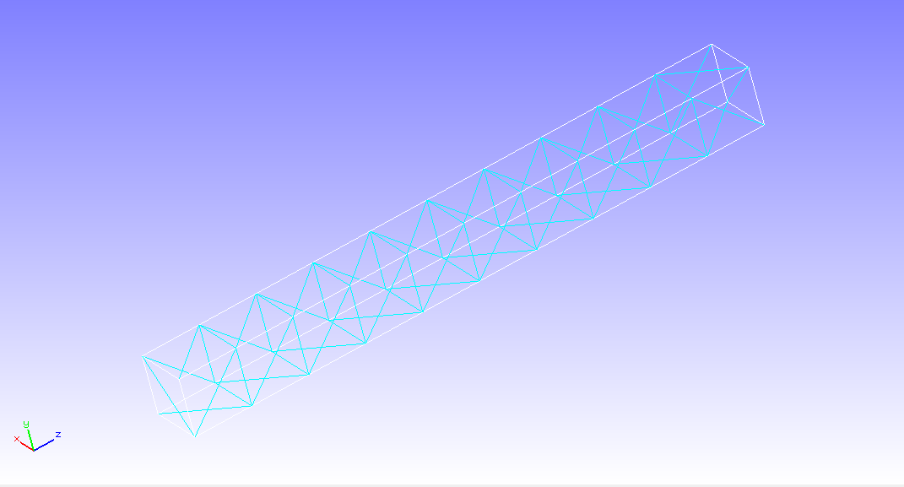
解析条件:


縦弾性係数	$E$	$210000\ N/mm^2$
ポアソン比	$\nu$	$0.3$
密度	$\rho$	$7.89E-09\ t/mm^3$
重力加速度	$g$	$9800.0\ mm/s^2$
荷重	$F_0$	$1.0\ N$
Rayleigh減衰のパラメータ	$R_m$	$0.0$
Rayleigh減衰のパラメータ	$R_k$	$7.2E-07$

図 9.1.15　解析モデル(4面体1次要素(要素数126、節点数55))

固有値解析から得られた5次までの固有値と加振点の周波数応答を示す。

モード	FrontISTR	ABAQUS
1	14952	14952
2	15002	15003
3	84604	84539
4	84771	84697
5	127054	126852

加振点の変位強度の周波数依存性

図 9.1.16　加振点の変位強度の周波数依存性

単純形状モデルによる検証