Verification by Simple Geometric Model

Verification by Simple-Shaped Model

Elastic static analysis

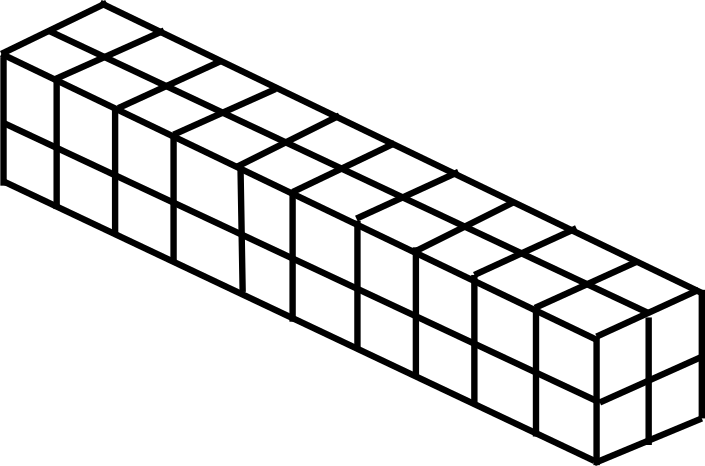
This verification was performed with a mesh-divided cantilever, as shown in Fig. 9.1.1. The analysis was performed with seven load conditions, exA–exG, as illustrated in Fig. 9.1.2. Please note that exG has the same load conditions as those of exA using the direct method solver.

The verification result of each load condition is presented in Tables 9.1.1–9.1.7.

Example of Mesh Partitioned Cantilever Beam (Hexahedral Element)

Fig. 9.1.1: Example of Mesh Partitioned Cantilever Beam (Hexahedral Element)


	(a) exA, G: Concentrated load
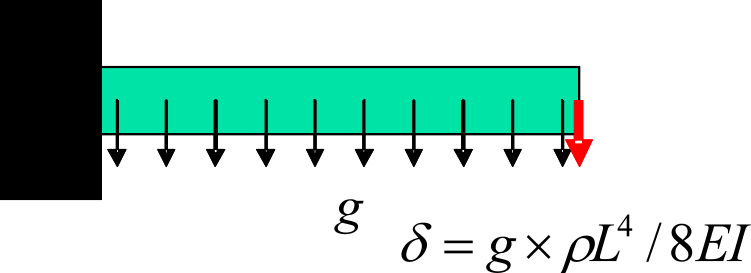	(b) exD: Gravitation
	(c) exB: Surface-distributed load
	(d) exE: Centrifugal force
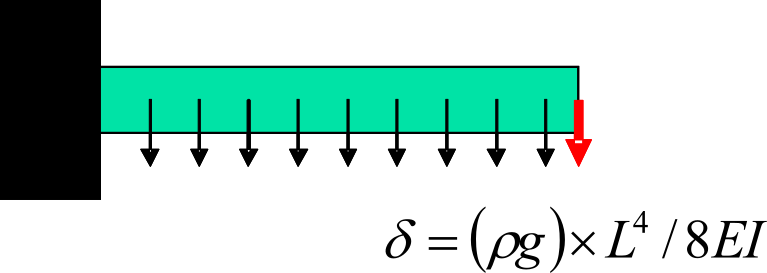	(e) exC: Volume load
	(f) exF : Heat load

Item	Value
Young's Modulus	$E = 4000.0\ kgf/mm^2$
Length	$L = 10.0\ mm$
Poisson's Ratio	$\nu = 0.3$
Sectional area	$A = 1.0\ mm^2$
Mass density	$\rho = 8.0102 \times 10^{-10}\ kg\,s^2/mm^4$
Second moment of area	$I = 1.0/12.0\ mm^4$
Gravitational acceleration	$g = 9800.0\ mm/s^2$
Linear coefficient of thermal expansion	$\alpha = 1.0 \times 10^{-5}$

Fig. 9.1.2: Verification conditions of the cantilever model

Table 9.1.1: exA: Verification results of the concentrated load problem

Case Name	Number of elements		Predicated Value : $\delta_{max}= -1.000$		Remarks
		NASTRAN	ABAQUS	FrontISTR
A231	40	-0.338	-0.371	-0.371	33 nodes / plane stress status problem
A232	40	-0.942	-1.002	-1.002	105 nodes / plane stress status problem
A241	20	-0.720	-0.711	-0.711	33 nodes / plane stress status problem
A242	20	-0.910	-1.002	-1.002	85 nodes / plane stress status problem
A341	240	-0.384	-0.384	-0.386	99 nodes
A342	240	-0.990	-0.990	-0.999	525 nodes
A351	80	-0.353	-0.355	-0.351	99 nodes
A352	80	-0.993	-0.993	-0.992	381 nodes
A361	40	-0.954	-0.985	-0.984	99 nodes
A362	40	-0.994	-0.993	-0.993	220 nodes
A731	40	-	-	-0.991	33 nodes / direct method
A741	20	-	-	-0.996	33 nodes / direct method

Table 9.1.2: exB: Verification results of the surface-distributed load problem

Case name	Number of elements		Predicated value : $\delta_{max}= -3.750$		Remarks
		NASTRAN	ABAQUS	FrontISTR
B231	40	-1.281	-1.403	-1.403	33 nodes / plane stress status problem
B232	40	-3.579	-3.763	-3.763	105 nodes / plane stress status problem
B241	20	-3.198	-2.680	-2.680	33 nodes / plane stress status problem
B242	20	-3.426	-3.765	-3.765	85 nodes / plane stress status problem
B341	240	-1.088	-1.449	-1.454	99 nodes
B342	240	-3.704	-3.704	-3.748	525 nodes
B351	80	-3.547	-1.338	-1.325	99 nodes
B352	80	-0.3717	-3.716	-3.713	381 nodes
B361	40	-3.557	-3.691	-3.688	99 nodes
B362	40	-3.726	-3.717	-3.717	220 nodes
B731	40	-	-	-3.722	33 nodes / direct method
B741	20	-	-	-3.743	33 nodes / direct method

Table 9.1.3: exC: Verification results of the volume load problem

Case Name	Number of elements		Predicated Value : $\delta_{max}= -2.944^{-5}$		Remarks
		NASTRAN	ABAQUS	FrontISTR
C231	40	-	-1.101e-5	-1.101e-5	33 nodes / plane stress problem
C232	40	-	-2.951e-5	-2.951e-5	105 nodes / plane stress problem
C241	20	-	-2.102e-5	-2.102e-5	33 nodes / plane stress problem
C242	20	-	-2.953e-5	-2.953e-5	85 nodes / plane stress problem
C341	240	-	-1.136e-5	-1.140e-5	99 nodes
C342	240	-	-2.905e-5	-2.937e-5	525 nodes
C351	80	-	-1.050e-5	-1.039e-5	99 nodes
C352	80	-	-2.914e-5	-2.911e-5	381 nodes
C361	40	-	-2.895e-5	-2.893e-5	99 nodes
C362	40	-	-2.915e-5	-2.915e-5	220 nodes
C731	40	-	-	-2.922e-5	33 nodes / direct method
C741	20	-	-	-2.938e-5	33 nodes / direct method

Table 9.1.4: exD: Verification results of the gravitation problem

Case name	Number of elements		Predicated Value : $\delta_{max}= -2.944^{-5}$		Remarks
		NASTRAN	ABAQUS	FrontISTR
D231	40	-1.101e-5	-1.101e-5	-1.101e-5	33 nodes / plane stress status problem
D232	40	-2.805e-5	-2.951e-5	-2.951e-5	105 nodes / plane stress status problem
D241	20	-2.508e-5	-2.102e-5	-2.102e-5	33 nodes / plane stress status problem
D242	20	-2.684e-5	-2.953e-5	-2.953e-5	85 nodes / plane stress status problem
D341	240	-1.172e-5	-1.136e-5	-1.140e-5	99 nodes
D342	240	-2.906e-5	-2.905e-5	-2.937e-5	525 nodes
D351	80	-1.046e-5	-1.050e-5	-1.039e-5	99 nodes
D352	80	-2.917e-5	-2.914e-5	-2.911e-5	381 nodes
D361	40	-2.800e-5	-2.895e-5	-2.893e-5	99 nodes
D362	40	-2.919e-5	-2.915e-5	-2.915e-5	220 nodes
D731	40	-	-	-2.922e-5	33 nodes / direct method
D741	20	-	-	-2.938e-5	33 nodes / direct method

Table 9.1.5: exE: Verification results of the centrifugal force problem

Case name	Number of elements		Predicated value : $\delta_{max}= 2.635^{-3}$		Remarks
		NASTRAN	ABAQUS	FrontISTR
E231	40	2.410e-3	2.616e-3	2.650e-3	33 nodes / plane stress status problem
E232	40	2.447e-3	2.627e-3	2.628e-3	105 nodes / plane stress status problem
E241	20	2.386e-3	2.622e-3	2.624e-3	33 nodes / plane stress status problem
E242	20	2.387e-3	2.627e-3	2.629e-3	85 nodes / plane stress status problem
E341	240	2.708e-3	2.579e-3	2.625e-3	99 nodes
E342	240	2.639e-3	2.614e-3	2.638e-3	525 nodes
E351	80	2.642e-3	2.598e-3	2.625e-3	99 nodes
E352	80	2.664e-3	2.617e-3	2.616e-3	381 nodes
E361	40	2.611e-3	2.603e-3	2.603e-3	99 nodes
E362	40	2.623e-3	2.616e-3	2.616e-3	220 nodes
E731	40	-	-	2.619e-3	33 nodes / direct method
E741	20	-	-	2.622e-3	33 nodes / direct method

Table 9.1.6: exF: Verification results of the thermal stress load problem

Case name	Number of elements		Predicated Value : $\delta_{max}= 1.000^{-2}$		Remarks
		NASTRAN	ABAQUS	FrontISTR
F231	40	-	1.016e-2	1.007e-2	33 nodes / plane stress status problem
F232	40	-	1.007e-2	1.007e-2	105 nodes / plane stress status problem
F241	20	-	1.010e-2	1.010e-2	33 nodes / plane stress status problem
F242	20	-	1.006e-2	1.006e-2	85 nodes / plane stress status problem
F341	240	-	1.047e-2	1.083e-2	99 nodes
F342	240	-	1.018e-2	1.022e-2	525 nodes
F351	80	-	1.031e-2	1.062e-2	99 nodes
F352	80	-	1.015e-2	1.017e-2	381 nodes
F361	40	-	1.026e-2	1.026e-2	99 nodes
F362	40	-	1.016e-2	1.016e-2	220 nodes

Table 9.1.7: exG: Verification results of the direct method (concentrated load problem)

Case name	Number of elements		Predicated value : $\delta_{max}= -1.000$		Remarks
		NASTRAN	ABAQUS	FrontISTR
G231	40	-0.338	-0.371	-0.371	33 nodes / plane stress status problem
G232	40	-0.942	-1.002	-1.002	105 nodes / plane stress status problem
G241	20	-0.720	-0.711	-0.711	33 nodes / plane stress status problem
G242	20	-0.910	-1.002	-1.002	85 nodes / plane stress status problem
G341	240	-0.384	-0.384	-0.386	99 nodes
G342	240	-0.990	-0.990	-0.999	52 nodes
G351	80	-0.353	-0.355	-0.351	99 nodes
G352	80	-0.993	-0.993	-0.992	381 nodes
G361	40	-0.954	-0.985	-0.984	99 nodes
G362	40	-0.994	-0.993	-0.993	220 nodes
G731	40	-	-	-0.991	33 nodes / direct method
G741	20	-	-	-0.996	33 nodes / dierct method

Non-linear static analysis

(2-1) exnl1: Geometrical non-linear analysis

The verification model of exI is the same as those of exA–G. A schematic diagram of the verification model is shown in Fig. 9.1.3. A geometric non-linear analysis was performed on this model. The verification results are presented in Table 9.1.8.

The non-linear calculation is a ten-step process with an increment value of 0.1 P and a final load of 1.0 P.

Verification model

Fig. 9.1.3: Verification model

Table 9.1.8: exI: Verification results (maximum deflection amount log)

Case Name	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	Linear Solution
I231	-	-	-	-	-	-	-	-	-	-	-
I232	-	-	-	-	-	-	-	-	-	-	-
I241	-	-	-	-	-	-	-	-	-	-	-
I242	-	-	-	-	-	-	-	-	-	-	-
I341	0.039	0.077	0.116	0.154	0.193	0.232	0.270	0.309	0.348	0.386	0.386
I342	0.099	0.200	0.300	0.400	0.499	0.599	0.698	0.797	0.896	0.995	0.999
I351	0.035	0.070	0.105	0.141	0.176	0.211	0.246	0.281	0.316	0.351	0.351
I352	0.099	0.198	0.298	0.397	0.496	0.595	0.693	0.792	0.890	0.987	0.992
I361	0.070	0.139	0.209	0.278	0.348	0.417	0.487	0.556	0.625	0.694	0.984
I362	0.099	0.197	0.298	0.397	0.496	0.595	0.694	0.793	0.891	0.988	0.993

(2-2) exnl2: Elastoplasticity deformation analysis

Based on the test conducted at National Agency for Finite Element Methods and Standards (NAFEMS; U.K.): Test NL1, this verification problem was verified by elastoplastic deformation analysis that incorporated geometric non-linearity and multiple hardening rules. The elastoplastic deformation analysis model is shown in Fig. 9.1.4.

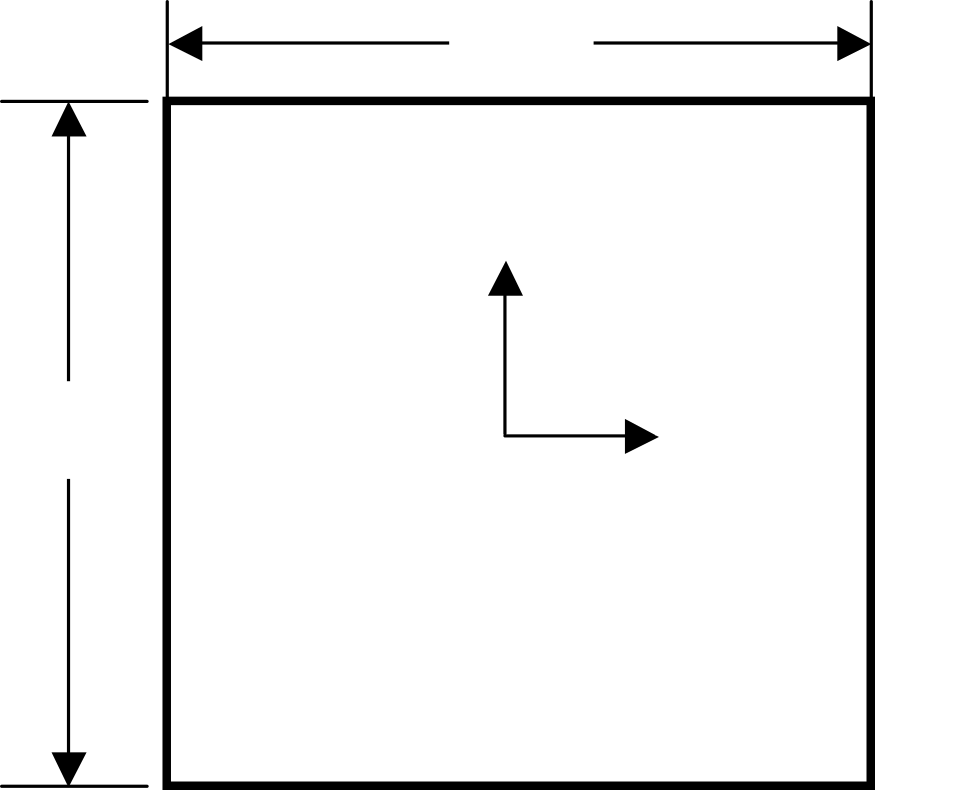
Elastoplasticity deformation analysis Model

Fig. 9.1.4: Elastoplasticity deformation analysis Model

(1) Verification conditions:

Item	Value
Material	Mises elastoplastic material
Young's Modulus	$E = 250 GPa$
Poisson's Ratio	$\nu = 0.25$
Initial yield stress	$5 MPa$
Initial yield strain	$0.25\times 10^{-4}$
Isotropic hardening factor	$H_i = 0$ or $62.5 GPa$

(2) Boundary conditions

Item	Boundary conditions	Value
step 1	Forced displacement in nodes 2 and 3	$u_x = 0.2500031251 *10^{-4}$
step 2	Forced displacement in nodes 2 and 3	$u_x = 0.25000937518*10^{-4}$
step 3	Forced displacement in nodes 3 and 4	$u_y = 0.2500031251 *10^{-4}$
step 4	Forced displacement in nodes 3 and 4	$u_y = 0.25000937518*10^{-4}$
step 5	Forced displacement in nodes 2 and 3	$u_x = -0.25000937518*10^{-4}$
step 6	Forced displacement in nodes 2 and 3	$u_x = -0.2500031251 *10^{-4}$
step 7	Forced displacement in nodes 3 and 4	$u_y = -0.25000937518*10^{-4}$
step 8	Forced displacement in nodes 3 and 4	$u_y = -0.2500031251 *10^{-4}$

All the nodes that are not mentioned here are fully constrained. The theoretical solution for this problem is presented as follows:

Strain ( $\times10^{-4}$ ) [ $\varepsilon_x$ , $\varepsilon_y$ , $\varepsilon_z$ ]	Equivalent Stress ( $MPa$ ) [ $H_i=0\ H_k=0$ ; $H_i=62.5\ H_k=0$ ]
0.25, 0, 0	5.0; 5.0
0.50, 0, 0	5.0; 5.862
0.50, 0.25, 0	5.0; 5.482
0.50, 0.50, 0	5.0; 6.362
0.25, 0.50, 0	5.0; 6.640
0, 0.50, 0	5.0; 7.322
0, 0.25, 0	3.917; 4.230
0, 0, 0	5.0; 5.673

The results of the calculations are as follows:

Strain ( $\times10^{-4}$ ) [ $\varepsilon_x$ , $\varepsilon_y$ , $\varepsilon_z$ ]	Equivalent Stress ( $MPa$ ) [ $H_i=0\ H_k=0$ ; $H_i=62.5\ H_k=0$ ]
0.25, 0, 0	5.0 (0.0%); 5.0 (0.0%)
0.50, 0, 0	5.0 (0.0%); 5.862 (0.0%)
0.50, 0.25, 0	5.0 (0.0%); 5.482 (0.0%)
0.50, 0.50, 0	5.0 (0.0%); 6.362 (-0.05%)
0.25, 0.50, 0	5.0 (0.0%); 6.640 (-0.21%)
0, 0.50, 0	5.0 (0.0%); 7.322 (-0.34%)
0, 0.25, 0	3.824 (-2.4%); 4.230 (-2.70%)
0, 0, 0	5.0 (0.0%); 5.673 (5.673 (-2.50%)

Contact analysis (1)

Based on the contact patch test problem (CGS-4) from NAFEMS (U.K.), this verification problem tests the finite sliding contact problem function with friction. The contact analysis model is shown in Fig. 9.1.5

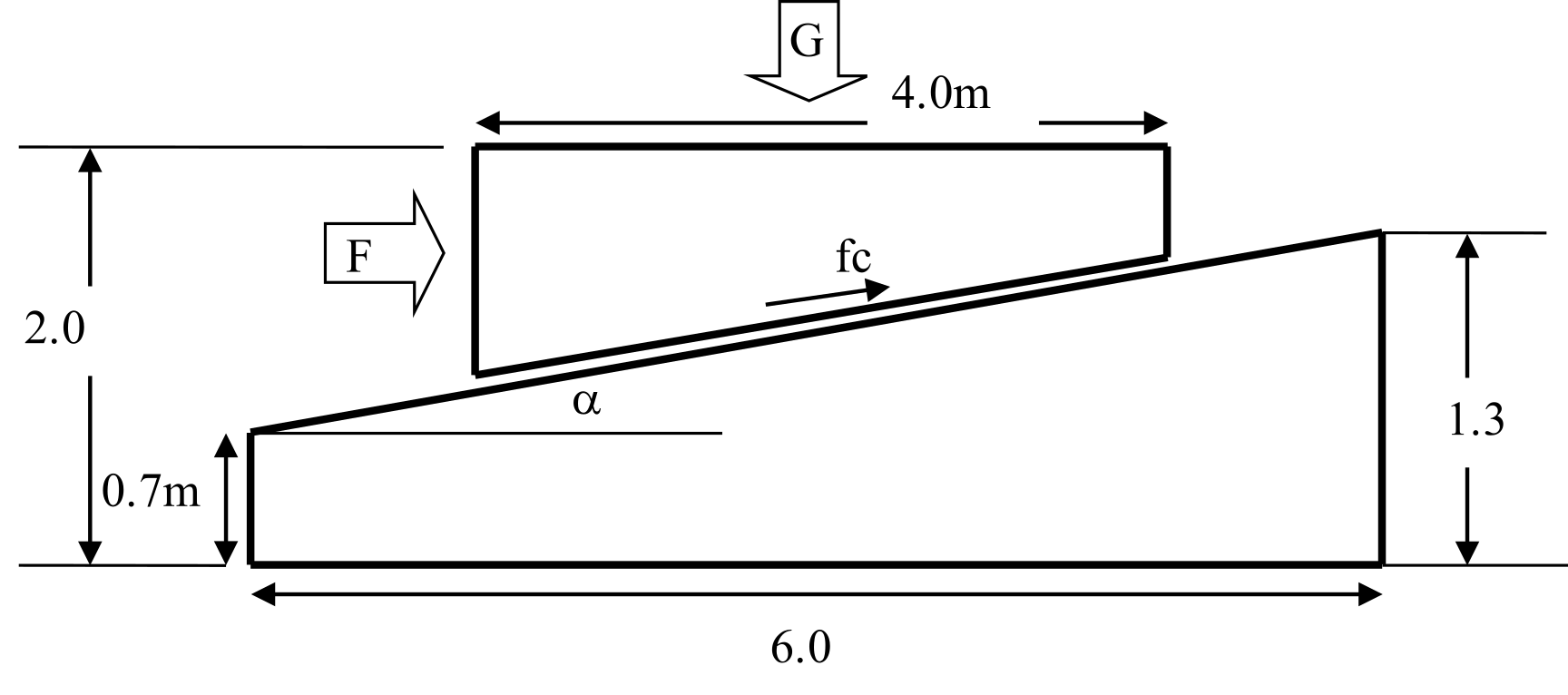
Contact analysis model

Fig. 9.1.5: Contact analysis model

The equilibrium condition of this problem is as follows:

$Fcos\,\alpha - Gsin\,\alpha = \pm f_{c}$

In the adhesive friction stage, the frictional force is as follows:

$f_{c} = E_t\Delta u$

In the sliding friction stage, the frictional force is as follows:

$f_c = \mu(G \cos\,\alpha + F \sin\,\alpha)$

The comparison between the calculation results and the analysis solution is as follows.

$\mu$	$F/G$ Analysis Solution	$F/G$ Calculation Results
0.0	0.1	0.1
0.1	0.202	0.202
0.2	0.306	0.306
0.3	0.412	0.412

Contact analysis (2): Hertz contact problem

In this verification, the Hertz contact problem between a cylinder of infinite length and an infinite plane was analyzed. The cylinder’s radius was R=8 mm, and the deformable body’s Young’s modulus E and Poisson’s ratio µ were 1100 MPa and 0.0, respectively. Moreover, assuming that the contact area was much smaller than the cylinder’s radius, and also considering the symmetry of the problem, the analysis was performed with a quarter model of the cylinder.

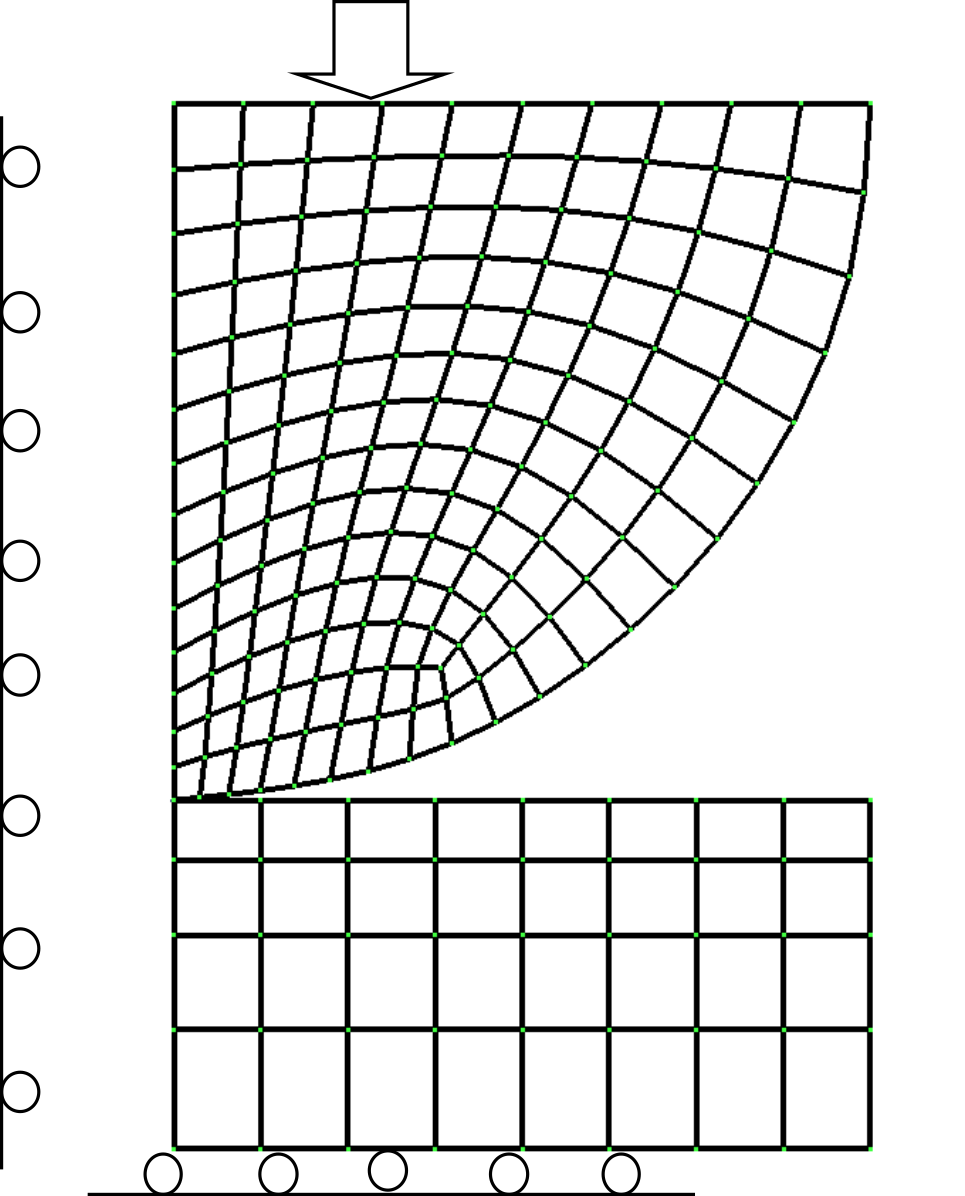
Hertz contact problem analysis model

Fig. 9.1.6: Hertz contact problem analysis model

(1) Verification results of contact radius

The theoretical formula to calculate the contact radius is as follows:

$a = \sqrt{\frac{4FR}{\pi E^{*}}}$

where

$E^{*} = \frac{E}{2(1 - \mu^{2})}$

With the actual calculation, when the pressure is $F=100$ , the contact radius is $a=1.36$ .

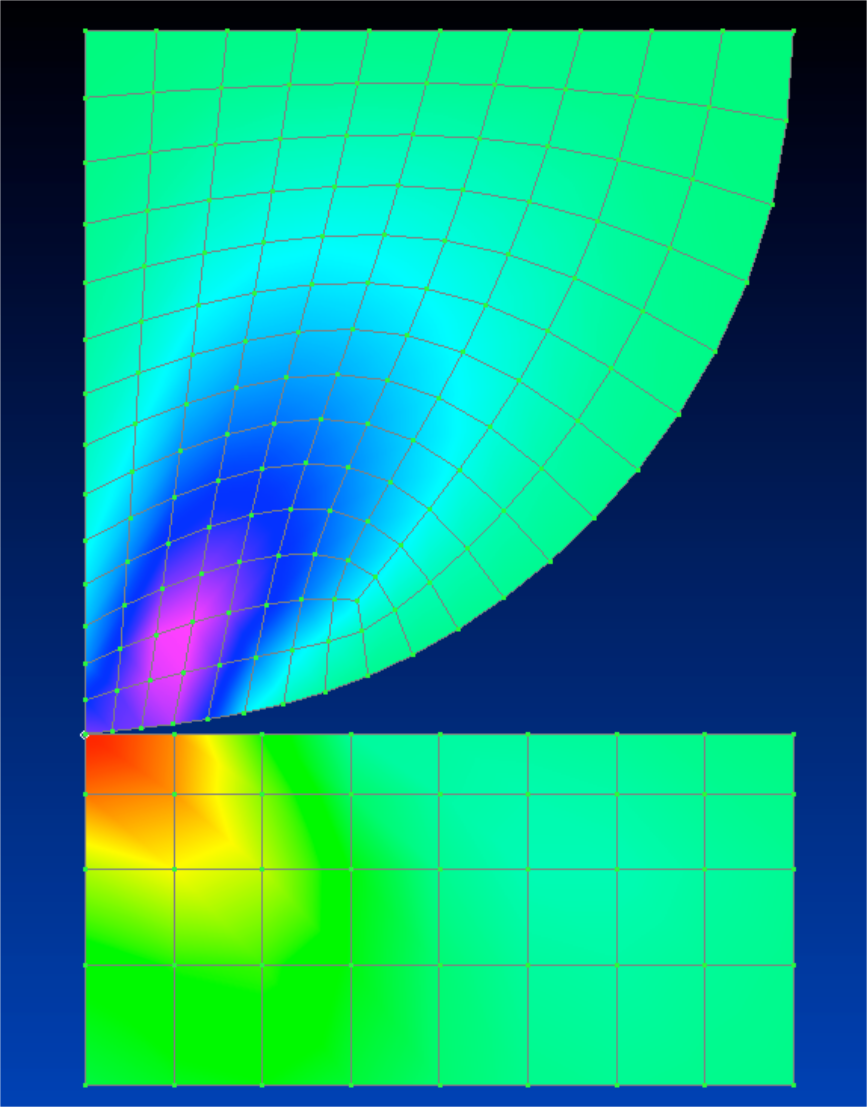
Fig. 9.1.7 shows the equivalent nodal force of the contact point. The contact radius is obtained by extrapolating this nodal force distribution.

Equivalent nodal force distribution of the contact point

Fig. 9.1.7: Equivalent nodal force distribution of the contact point

(2) Verification results of maximum shear stress

With the theoretical solution, when the contact position is $z=0.78a$ , the maximum shear stress is as follows:

$\tau_{max} = 0.30\sqrt{\frac{FE^*}{\pi R}}$

With the actual calculation conditions, it becomes

$\tau_{max} = 14.2$

The actual result obtained was

$\tau_{max} = 15.6$

Shear stress distribution (maximum value = 15.6)

Fig. 9.1.8: Shear stress distribution (maximum value = 15.6)

(3) Eigenvalue analysis

The verification models of exJ and exK are the same as those of exA–G. A schematic diagram of the verification model is shown in Fig. 9.1.9. An eigenvalue analysis was performed for this model to determine the primary, secondary, and tertiary eigenvalues. The iteration and direct method solvers were used for exJ and exK, respectively. Furthermore, the verification results are presented in Tables 9.1.9–9.1.12.

Verification Model

Fig. 9.1.9: Verification Model

The vibration eigenvalue of the cantilever is determined by the following equations:

Primary : $n_1 = \frac{1.875^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$

Secondary : $n_2 = \frac{4.694^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$

Tertiary : $n_3 = \frac{7.855^2}{2 \pi l^2} \sqrt{ \frac{gEI}{\omega} }$

The property values of the verification model are:

Item	Value
$I$	$10.0 mm$
$E$	$4000.0 kgf /mm^2$
$l$	$1.0/12.0 mm^4$
$\omega$	$7.85 * 10^{-6} kgf/mm^3$
$g$	$9800.0 mm/sec^2$

Therefore, the primary to tertiary eigenvalue are as follows:

Mode number	Value
$n_1$	3.609e3
$n_2$	2.262e4
$n_3$	6.335e4

Table 9.1.9: exJ: Iteration method verification results with the primary eigenvalue

Case Name	Number of elements	Predicated value : n1=3.609e3		Remarks
		NASTRAN	FrontISTR
J231	40	5.861e3	5.861e3	33 nodes / plane stress status problem
J232	40	3.596e3	3.593e3	105 nodes / plane stress status problem
J241	20	3.586e3	4.245e3	33 nodes / plane stress status problem
J242	20	3.590e3	3.587e3	85 nodes / plane stress status problem
J341	240	5.442e3	5.429e3	99 nodes
J342	240	3.621e3	3.595e3	525 nodes
J351	80	3.695e3	4.298e3	99 nodes
J352	80	3.610e3	3.609e3	381 nodes
J361	40	3.679e3	3.619e3	99 nodes
J362	40	3.611e3	3.606e3	220 nodes

Table 9.1.10: Iteration method verification results of exJ with the secondary eigenvalue

Case name	Number of elements	Predicated value : n2=2.262e4		Remarks
		NASTRAN	FrontISTR
J231	40	3.350e4	3.351e4	33 nodes / plane stress status problem
J232	40	2.163e4	2.156e4	105 nodes / plane stress status problem
J241	20	2.149e4	2.516e4	33 nodes / plane stress status problem
J242	20	2.149e4	2.143e4	85 nodes / plane stress status problem
J341	240	3.145e4	3.138e4	99 nodes
J342	240	2.171e4	2.155e4	525 nodes
J351	80	2.208e4	2.546e4	99 nodes
J352	80	2.156e4	2.149e4	381 nodes
J361	40	2.202e4	2.168e4	99 nodes
J362	40	2.154e4	2.144e4	220 nodes

Note: In the three-dimensional (3D) models, the primary and secondary values have equal roots. Therefore, the secondary value in the table represents the tertiary calculation value.

Table 9.1.11: Direct method verification results of exK with the primary eigenvalue

Case name	Number of elements	Predicated Value : n1=3.609e3		Remarks
		NASTRAN	FrontISTR
J231	40	5.861e3	5.861e3	33 nodes / plane stress status problem
J232	40	3.596e3	3.593e3	105 nodes / plane stress status problem
J241	20	3.586e3	4.245e3	33 nodes / plane stress status problem
J242	20	3.590e3	3.587e3	85 nodes / plane stress status problem
J341	240	5.442e3	5.429e3	99 nodes
J342	240	3.621e3	3.595e3	525 nodes
J351	80	3.695e3	4.298e3	99 nodes
J352	80	3.610e3	3.609e3	381 nodes
J361	40	3.679e3	3.619e3	99 nodes
J362	40	3.611e3	3.606e3	220 nodes
J731	40	-	3.606e3	220 nodes
J741	20	-	3.594e3	220 nodes

Table 9.1.12: Direct method verification results of exK with the secondary eigenvalue

Case name	Number of elements	Predicated value : n2=2.262e4		Remarks
		NASTRAN	FrontISTR
J231	40	3.350e4	3.351e4	33 nodes / plane stress status problem
J232	40	2.163e4	2.156e4	105 nodes / plane stress status problem
J241	20	2.149e4	2.516e4	33 nodes / plane stress status problem
J242	20	2.149e4	2.143e4	85 nodes / plane stress status problem
J341	240	3.145e4	3.138e4	99 nodes
J342	240	2.171e4	2.155e4	525 nodes
J351	80	2.208e4	2.546e4	99 nodes
J352	80	2.156e4	2.149e4	381 nodes
J361	40	2.202e4	2.168e4	99 nodes
J362	40	2.154e4	2.144e4	220 nodes
J731	40	-	2.156e4	220 nodes
J741	20	-	2.153e4	220 nodes

Note: In the 3D models, the primary and secondary values have equal roots. Therefore, the secondary value in the table represents the tertiary calculation value.

(4) Heat conduction analysis

The common conditions for the steady-state heat conduction analysis are shown in Fig. 9.1.10. The individual conditions for the verification cases exM–exT are shown in Fig. 9.1.11. The mesh division used here is equivalent to that of exA.

The verification results (temperature distribution table) of each case are presented in Tables 9.1.13–9.1.20.

Heat conduction analysis


Length between AB	$L = 10.0m$
Cross-sectional area	$A = 1.0 mm^2$

Temperature dependency of thermal conductivity

Thermal conductivity $\lambda(W/mK)$	Temperature $(^\circ C)$
50.0	0.0
35.0	500.0
20.0	1000.0

Fig. 9.1.10: Verification conditions of steady-heat conduction analysis


exM: Linear material
exN: Specified tempreature problem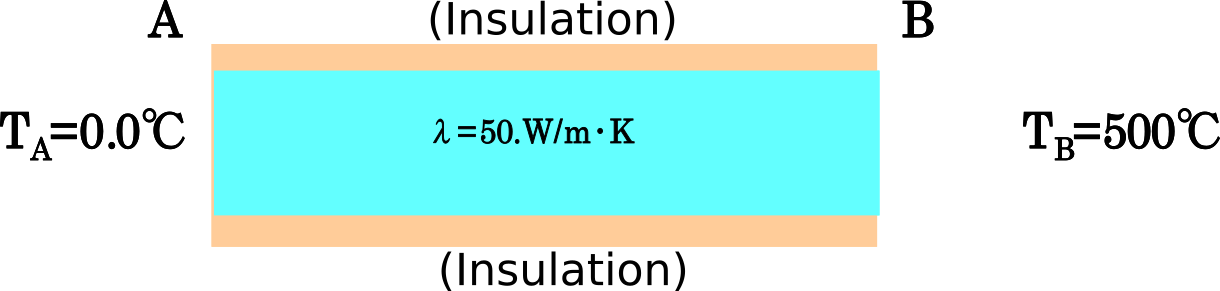
exO: Concentrated heat flux problem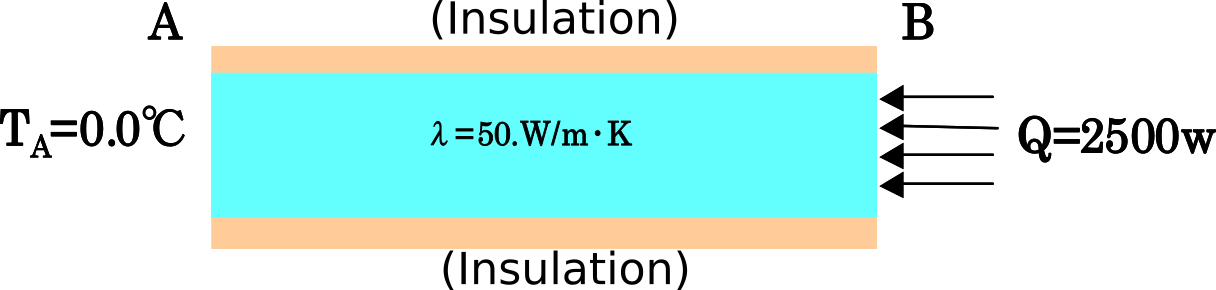
exP: Distributed heat flux problem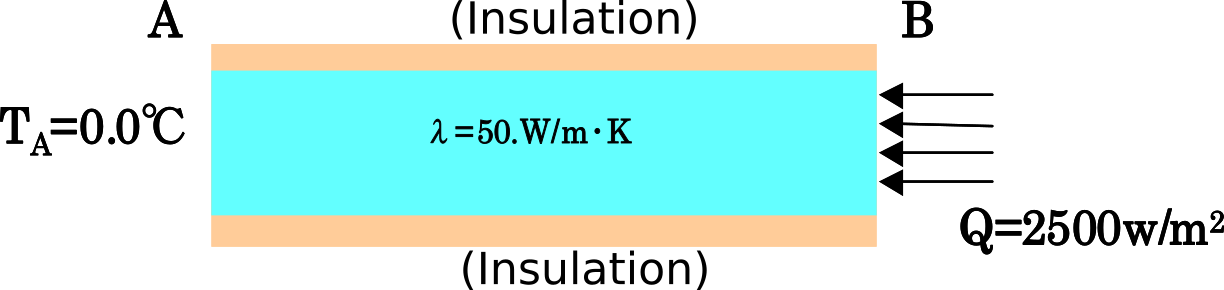
exQ: Convective heat transfer problem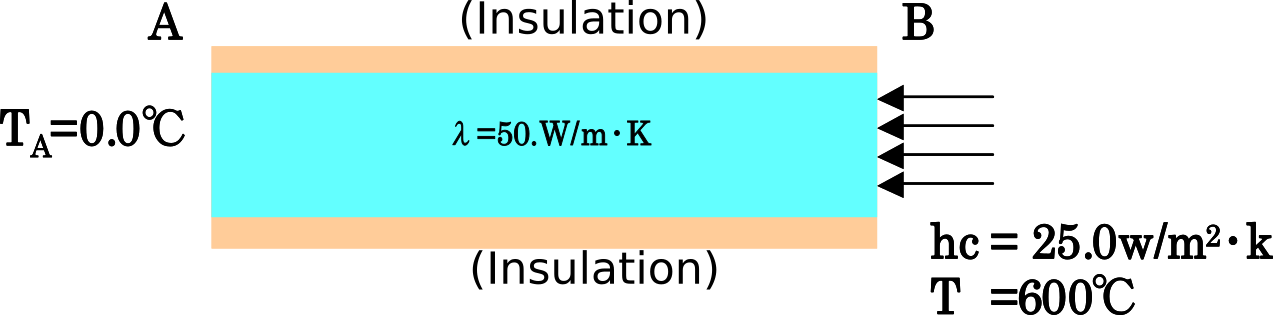
exR: Radiant heat transfer problem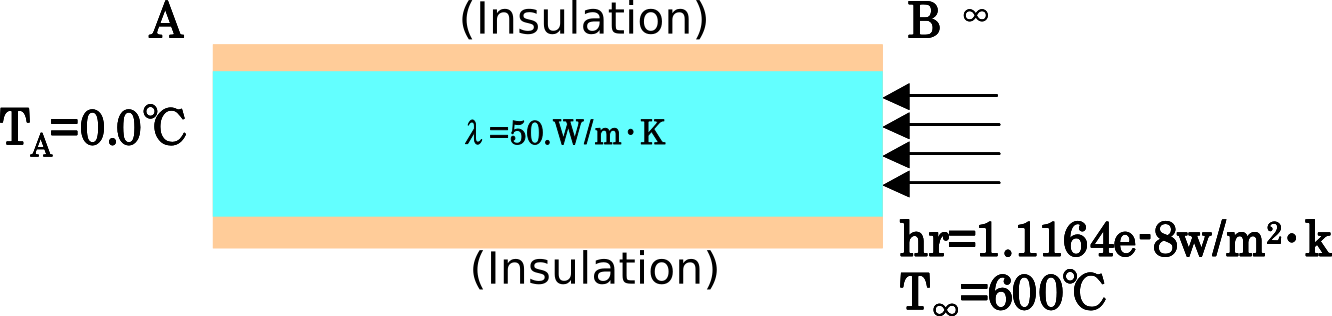
exS: Volume heat generation problem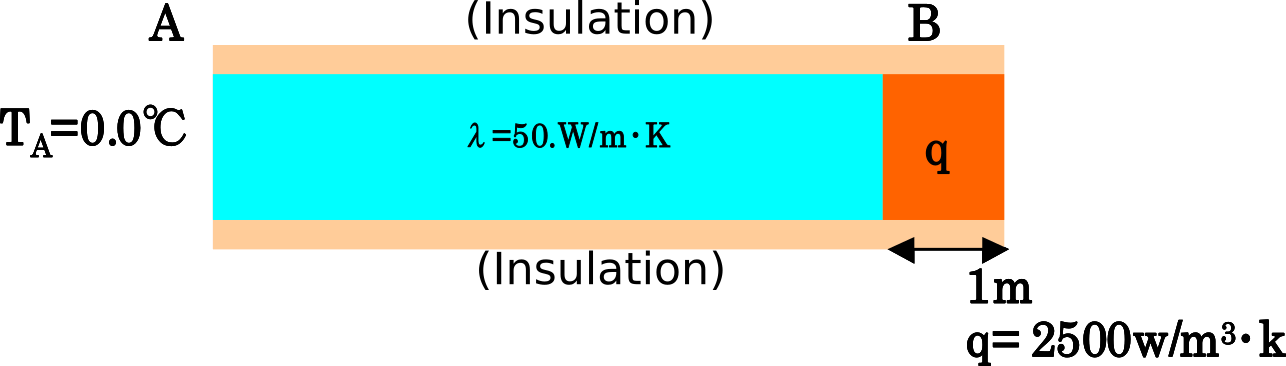
exT: Internal gap problem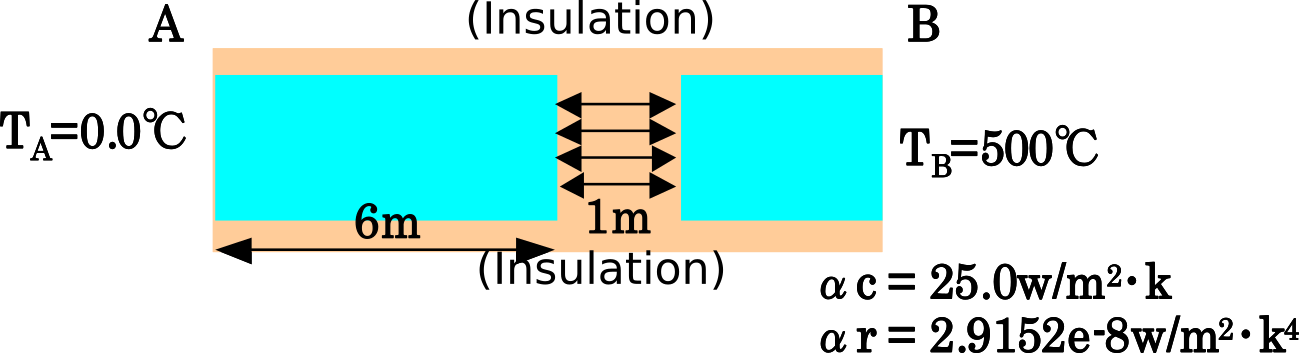

Fig. 9.1.11: Analysis conditions for each verification case

Table 9.1.13: Verification results of exM (steady-state calculation of linear material)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
M361A	361	40/33	0.0	100.0	200.0	300.0	400.0	500.0
M361B	361	40/105	0.0	100.0	200.0	300.0	400.0	500.0
M361C	361	20/33	0.0	100.0	200.0	300.0	400.0	500.0
M361D	361	20/85	0.0	100.0	200.0	300.0	400.0	500.0
M361E	361	240/99	0.0	100.0	200.0	300.0	400.0	500.0
M361F	361	24/525	0.0	100.0	200.0	300.0	400.0	500.0
M361G	361	80/99	0.0	100.0	200.0	300.0	400.0	500.0

Table 9.1.14: Verification results of exN (specified temperature problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	87.3	179.7	278.2	384.3	500.0
N231	231	40/33	0.0	87.2	179.5	278.0	384.1	500.0
N232	232	40/105	0.0	86.0	178.3	276.8	382.9	500.0
N241	241	20/33	0.0	87.3	179.7	278.2	384.3	500.0
N242	242	20/85	0.0	87.3	179.7	278.2	384.3	500.0
N341	341	240/99	0.0	87.3	179.7	278.2	384.3	500.0
N342	342	24/525	0.0	87.9	179.9	278.0	383.6	500.0
N351	351	80/99	0.0	87.3	179.7	278.2	384.3	500.0
N352	352	80/381	0.0	87.3	179.7	278.2	384.3	500.0
N361	361	40/99	0.0	87.3	179.7	278.2	384.3	500.0
N362	362	40/330	0.0	87.3	179.7	278.2	384.3	500.0
N731	731	40/33	0.0	87.3	179.7	278.2	384.3	500.0
N741	741	20/33	0.0	87.3	179.7	278.2	384.3	500.0

Table 9.1.15: Verification results of exO (concentrated heat flux problem)

Case name	Element type	Numbewr of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
O231	231	40/33	0.0	103.2	213.7	333.3	464.8	612.6
O232	232	40/105	0.0	103.2	213.7	333.3	464.8	612.6
O241	241	20/33	0.0	103.2	213.7	333.3	464.8	612.6
O242	242	20/85	0.0	103.2	213.7	333.4	465.2	618.0
O341	341	240/99	-	-	-	-	-	-
O342	342	24/525	0.0	104.4	214.9	334.7	466.3	614.6
O351	351	80/99	-	-	-	-	-	-
O352	352	80/381	0.0	103.2	213.7	333.3	465.0	624.2
O361	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
O362	362	40/330	0.0	103.2	213.7	333.4	465.5	623.5
O731	731	40/33	0.0	103.2	213.7	333.3	464.8	612.5
O741	741	20/33	0.0	103.2	213.7	333.3	464.8	612.6

Table 9.1.16: Verification results of exP (distribution heat flux problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
P231	231	40/33	0.0	103.2	213.7	333.3	464.8	612.6
P232	232	40/105	0.0	103.2	213.7	333.3	464.8	612.6
P241	241	20/33	0.0	103.2	213.7	333.3	464.8	612.6
P242	242	20/85	0.0	103.2	213.7	333.3	464.8	612.6
P341	341	240/99	-	-	-	-	-	-
P342	342	24/525	0.0	103.2	213.7	333.3	464.8	612.6
P351	351	80/99	-	-	-	-	-	-
P352	352	80/381	0.0	103.2	213.7	333.3	464.8	612.6
P361	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
P362	362	40/330	0.0	103.2	213.7	333.4	465.5	612.6
P731	731	40/33	0.0	103.2	213.7	333.3	464.8	612.5
P741	741	20/33	0.0	103.2	213.7	333.3	464.8	612.6

Table 9.1.17: Verification results of exQ (convective heat transfer problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	89.2	183.8	284.8	393.9	513.2
Q231	231	40/33	0.0	89.2	183.8	284.8	393.9	513.2
Q232	232	40/105	0.0	89.2	183.8	284.8	393.9	513.2
Q241	241	20/33	0.0	89.2	183.8	284.8	393.9	513.2
Q242	242	20/85	0.0	89.2	183.8	284.8	393.9	513.2
Q341	341	240/99	-	-	-	-	-	-
Q342	342	24/525	0.0	89.2	183.8	284.8	393.9	513.2
Q351	351	80/99	-	-	-	-	-	-
Q352	352	80/381	0.0	89.2	183.8	284.8	393.9	513.2
Q361	361	40/99	0.0	89.2	183.8	284.8	393.9	513.2
Q362	362	40/330	0.0	89.2	183.8	284.8	393.9	513.2
Q731	731	40/33	0.0	89.2	183.8	284.8	393.9	513.2
Q741	741	20/33	0.0	89.2	183.8	284.8	393.9	513.2

Table 9.1.18: Verification results of exR (radiation heat transfer problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	89.5	184.4	285.8	395.3	515.2
R231	231	40/33	0.0	89.5	184.4	285.8	395.3	515.2
R232	232	40/105	0.0	89.5	184.4	285.8	395.3	515.2
R241	241	20/33	0.0	89.5	184.4	285.8	395.3	515.2
R242	242	20/85	0.0	89.5	184.4	285.8	395.3	515.2
R341	341	240/99	-	-	-	-	-	-
R342	342	24/525	0.0	89.5	184.4	285.8	395.3	515.2
R351	351	80/99	-	-	-	-	-	-
R352	352	80/381	0.0	89.5	184.4	285.8	395.3	515.2
R361	361	40/99	0.0	89.5	184.4	285.8	395.3	515.2
R362	362	40/330	0.0	89.5	184.4	285.8	395.3	515.2
R731	731	40/33	0.0	89.5	184.4	285.8	395.3	515.2
R741	741	20/33	0.0	89.5	184.4	285.8	395.3	515.2

Table 9.1.19: Verification results of exS (volume heat generation problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
S231	231	40/33	0.0	103.2	213.7	333.3	464.8	612.6
S232	232	40/105	0.0	103.2	213.7	333.3	464.8	612.6
S241	241	20/33	0.0	103.2	213.7	333.3	464.8	612.6
S242	242	20/85	0.0	103.2	213.7	333.3	464.8	612.6
S341	341	240/99	-	-	-	-	-	-
S342	342	24/525	0.0	103.2	213.7	333.3	464.8	612.6
S351	351	80/99	-	-	-	-	-	-
S352	352	80/381	0.0	103.2	213.7	333.3	464.8	612.6
S361	361	40/99	0.0	103.2	213.7	333.3	464.8	612.6
S362	362	40/330	0.0	103.2	213.7	333.3	464.8	612.6
S731	731	40/33	0.0	103.2	213.7	333.3	464.8	612.6
S741	741	20/33	0.0	103.2	213.7	333.3	464.8	612.6

Table 9.1.20: Verification results of exT (internal gap problem)

Case name	Element type	Number of elements/nodes	Distance from edge A (m)
			Edge A	2.0	4.0	6.0	8,0	Edge B
ABAQUS	361	40/99	0.0	88.6	182.4	282.6	387.7	500.0
S231	231	40/33	0.0	88.6	182.4	282.6	387.7	500.0
S232	232	40/105	0.0	88.6	182.4	282.6	387.7	500.0
S241	241	20/33	0.0	88.6	182.4	282.6	387.7	500.0
S242	242	20/85	0.0	88.6	182.4	282.6	387.7	500.0
S341	341	240/99	-	-	-	-	-	-
S342	342	24/525	0.0	88.6	182.4	282.6	387.7	500.0
S351	351	80/99	-	-	-	-	-	-
S352	352	80/381	0.0	88.6	182.4	282.6	387.7	500.0
S361	361	40/99	0.0	88.6	182.4	282.6	387.7	500.0
S362	362	40/330	0.0	88.6	182.4	282.6	387.7	500.0
S731	731	40/33	0.0	88.6	182.4	282.6	387.7	500.0
S741	741	20/33	0.0	88.6	182.4	282.6	387.7	500.0

(5) Linear dynamic analysis

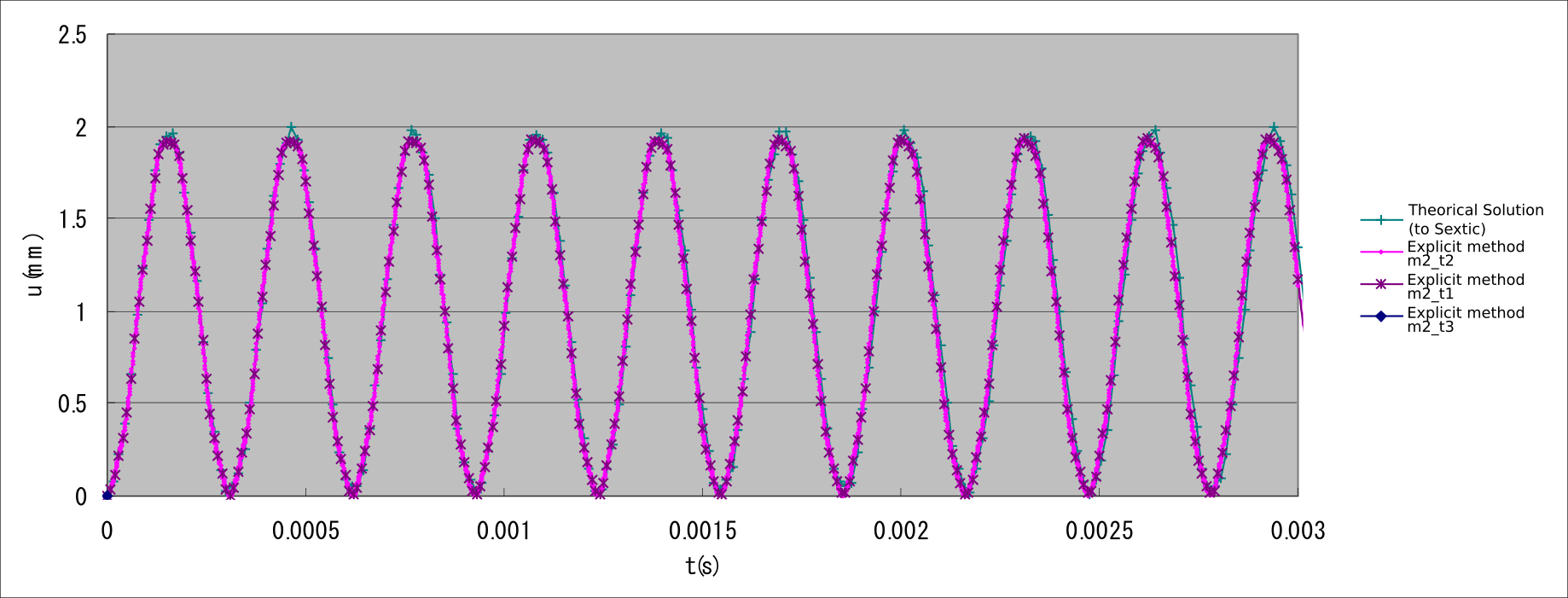
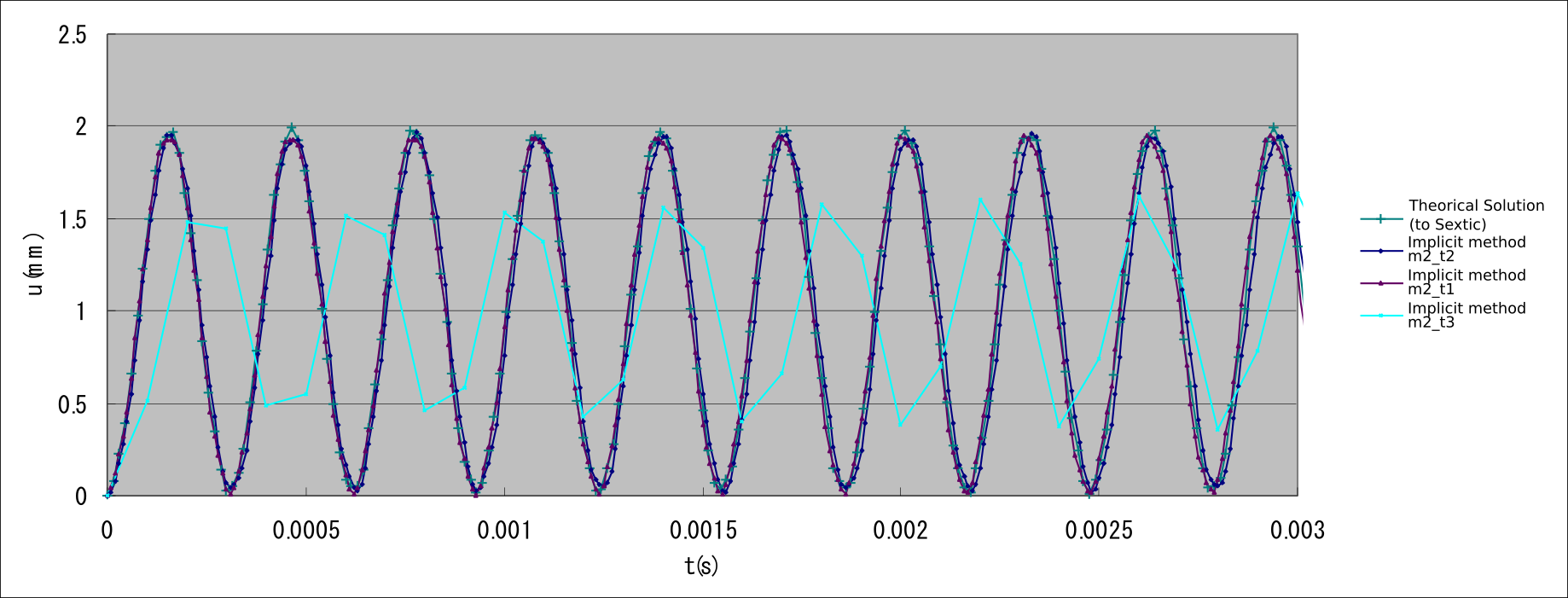
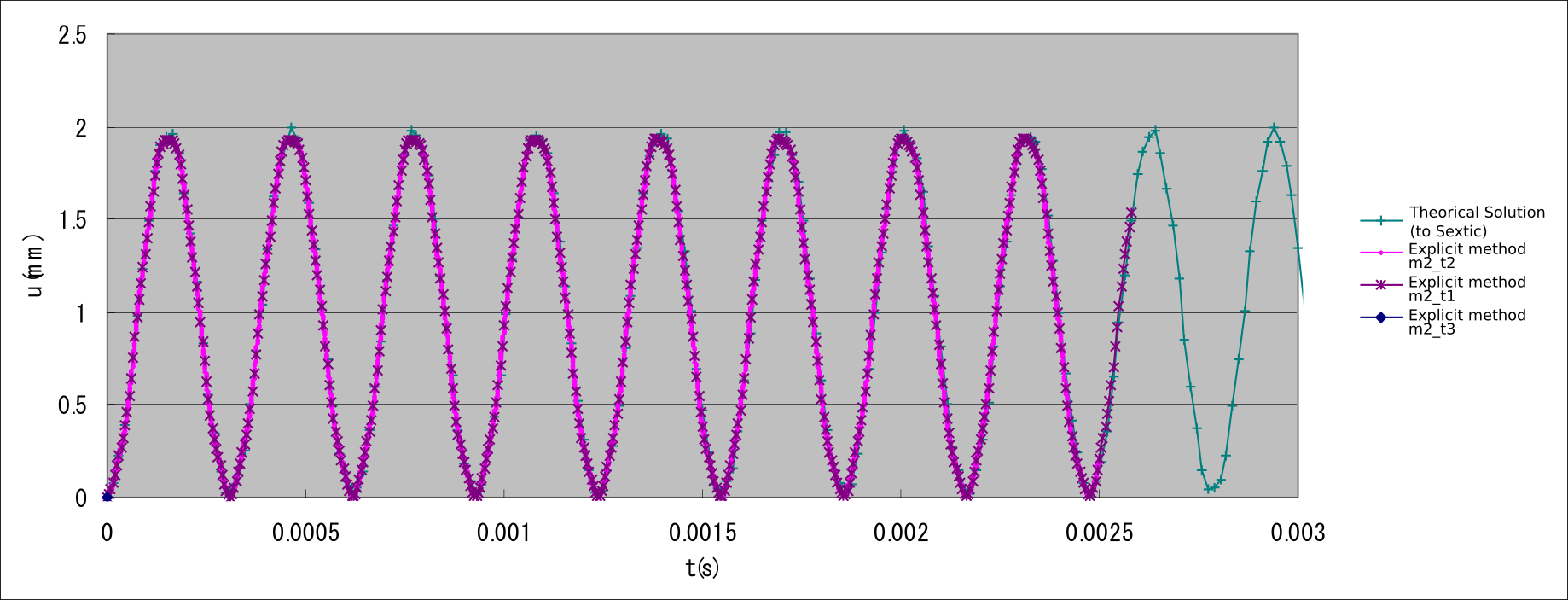
In exW, a linear dynamic analysis was performed on the same mesh-divided cantilever that was discussed earlier in the Elastic static analysis subsection, with the verification conditions shown in Fig. 9.1.12. The objective was to verify the impact of time increment on the results with the same mesh division. Both the implicit and explicit methods of dynamic analysis and the element types 361 and 342 were used. The verification results are presented in Table 9.1.22 and shown in Figs. 9.1.13–9.1.15.

Analysis Model

Time history of external force F

Time history of external force $F$

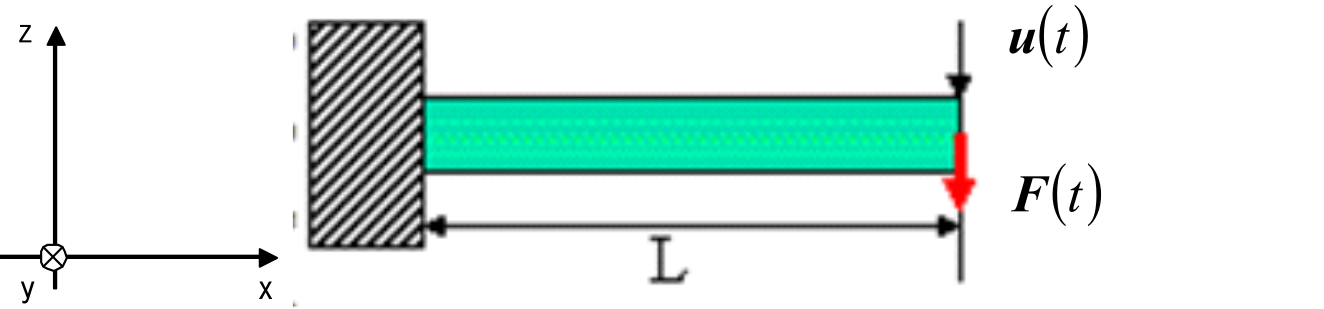
The theoretical solution for vibration point displacement is as follows:

$F(t)=F_0 I(t)$

where

$F_0:{\rm Constant\ vector}$

$I(t)= \begin{cases} 0, t < 0 \\\ 1, 0 \leq t \end{cases}$

$u(t) = \frac{F_0 l^3}{EI} \sum^{\infty}\_{i=1} \frac{1-\cos{\omega_i t}}{{\lambda_i}^4} \left\lbrace \cosh{\lambda_i}-\cos{\lambda_i}-\frac{\cosh{\lambda_i} + \cos{\lambda_i}}{\sin{\lambda_i}+\sin{\lambda_i}} (\sinh{\lambda_i} - \sin{\lambda_i}) \right\rbrace^2$

Fig. 9.1.12: Verification conditions of linear dynamic analysis

Verification conditions:


Length	$L$	$10.0\ mm$
Cross-sectional width	$a$	$1.0\ mm$
Cross-sectional height	$b$	$1.0\ mm$
Young's modulus	$E$	$4000.0\ kgf/mm^2$
Poisson's ratio	$\nu$	$0.3$
Density	$\rho$	$1.0E-09\ kgf\,s^2/mm^3$
Gravitational acceleration	$g$	$9800.0\ mm/s^2$
External force	$F_0$	$1.0\ kgf$


Element	Hexahedral linear element
Tetrahedral secondary element
Solution	Implicit method
Parameter $\gamma$ of Newmark- $\beta$ method	1/2
Parameter $\beta$ of Newmark- $\beta$ method	1/4
Explicit method
Damping	N/A

Table 9.1.21: Verification conditions of the linear dynamic analysis (continuation)

Case Name	Element Type	No. of Nodes	No. of Elements	Solution	Time Increment $\Delta t$ [sec]
W361_c0_im_m2_t1	361	99	40	Implicit method	1.0E-06
W361_c0_im_m2_t2	361	99	40	Implicit method	1.0E-05
W361_c0_im_m2_t3	361	99	40	Implicit method	1.0E-04
W361_c0_ex_m2_t1	361	99	40	Explicit method	1.0E-08
W361_c0_ex_m2_t2	361	99	40	Explicit method	1.0E-07
W361_c0_ex_m2_t3	361	99	40	Explicit method	1.0E-06
W342_c0_im_m2_t1	342	525	240	Implicit method	1.0E-06
W342_c0_im_m2_t2	342	525	240	Implicit method	1.0E-05
W342_c0_im_m2_t3	342	525	240	Implicit method	1.0E-04
W342_c0_ex_m2_t1	342	525	240	Explicit method	1.0E-08
W342_c0_ex_m2_t2	342	525	240	Explicit method	5.0E-08
W342_c0_ex_m2_t3	342	525	240	Explicit method	1.0E-07

Table 9.1.22: Verification results of linear dynamic analysis of exW (cantilever)

Case name	Element type	Number of nodes	Number of elements	Solution	z-direction displacement: $u_z(mm)$ when time $t = 0.002(s)$
					Theorical solution repeated to sextic equation	FrontISTR
W361_c0_im_m2_t1	361	99	40	Implicit method	1.9753	1.9302
W361_c0_im_m2_t2	361	99	40	Implicit method	1.9753	1.8686
W361_c0_im_m2_t3	361	99	40	Implicit method	1.9753	0.3794
W361_c0_ex_m2_t1	361	99	40	Explicit method	1.9753	1.9302
W361_c0_ex_m2_t2	361	99	40	Explicit method	1.9753	1.9247
W361_c0_ex_m2_t3	361	99	40	Explicit method	1.9753	Divergence
W342_c0_im_m2_t1	342	525	240	Implicit method	1.9753	1.9431
W342_c0_im_m2_t2	342	525	240	Implicit method	1.9753	1.8719
W342_c0_im_m2_t3	342	525	240	Implicit method	1.9753	0.3873
W342_c0_ex_m2_t1	342	525	240	Explicit method	1.9753	1.9359
W342_c0_ex_m2_t2	342	525	240	Explicit method	1.9753	1.9358
W342_c0_ex_m2_t3	342	525	240	Explicit method	1.9753	Divergence

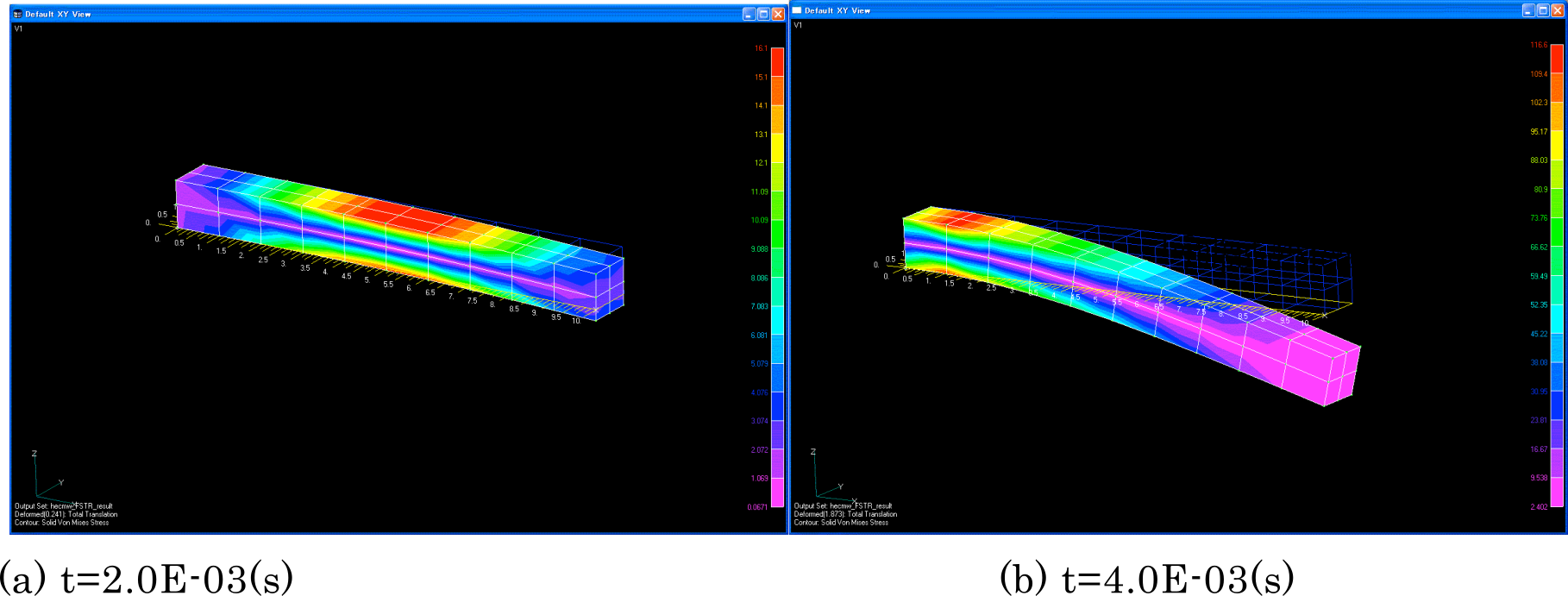
Deformation diagram and equivalent stress distribution of the cantilever (W361_c0_im_m2_t2)

Fig. 9.1.13: Deformation diagram and equivalent stress distribution of the cantilever (W361_c0_im_m2_t2)

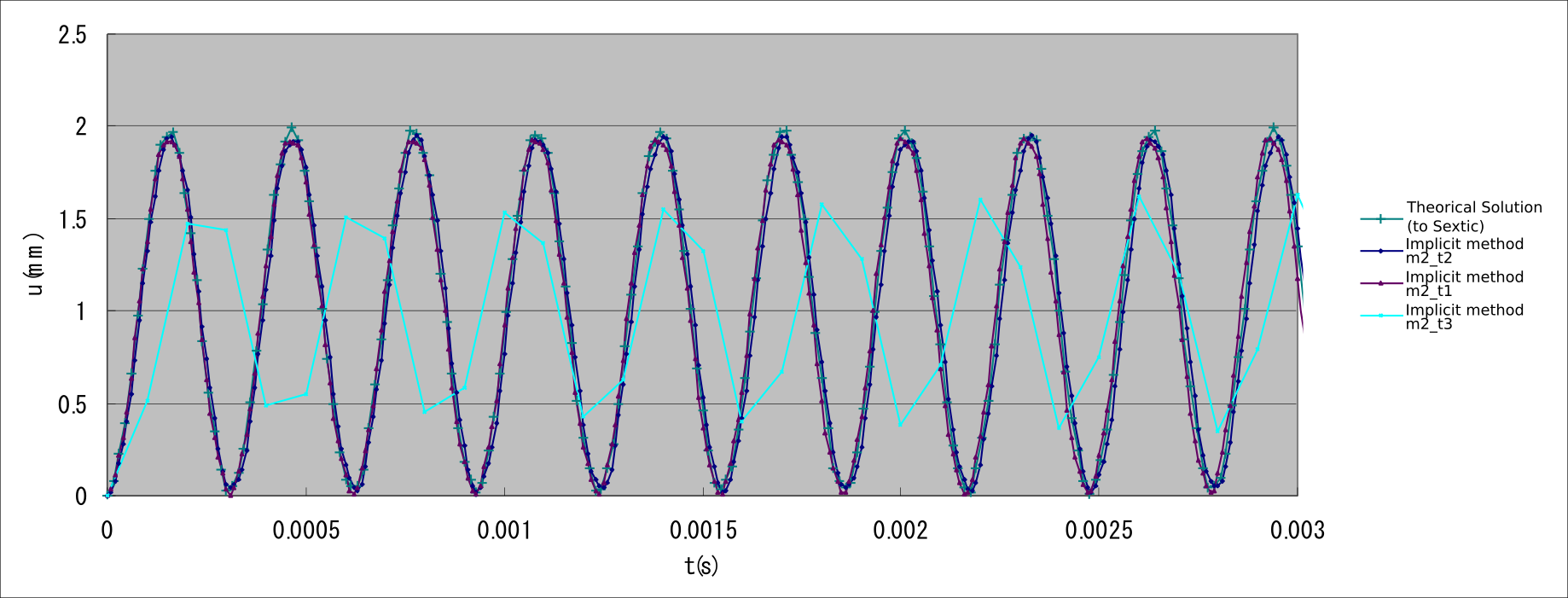
(a) Element Type 361 : Implicit method

(b) Element Type 361 : Explicit method

Fig. 9.1.14: Time history of vibration point displacement $u_z$

(a) Element Type 342 : Implicit method

(b) Element Type 342 : Explicit method

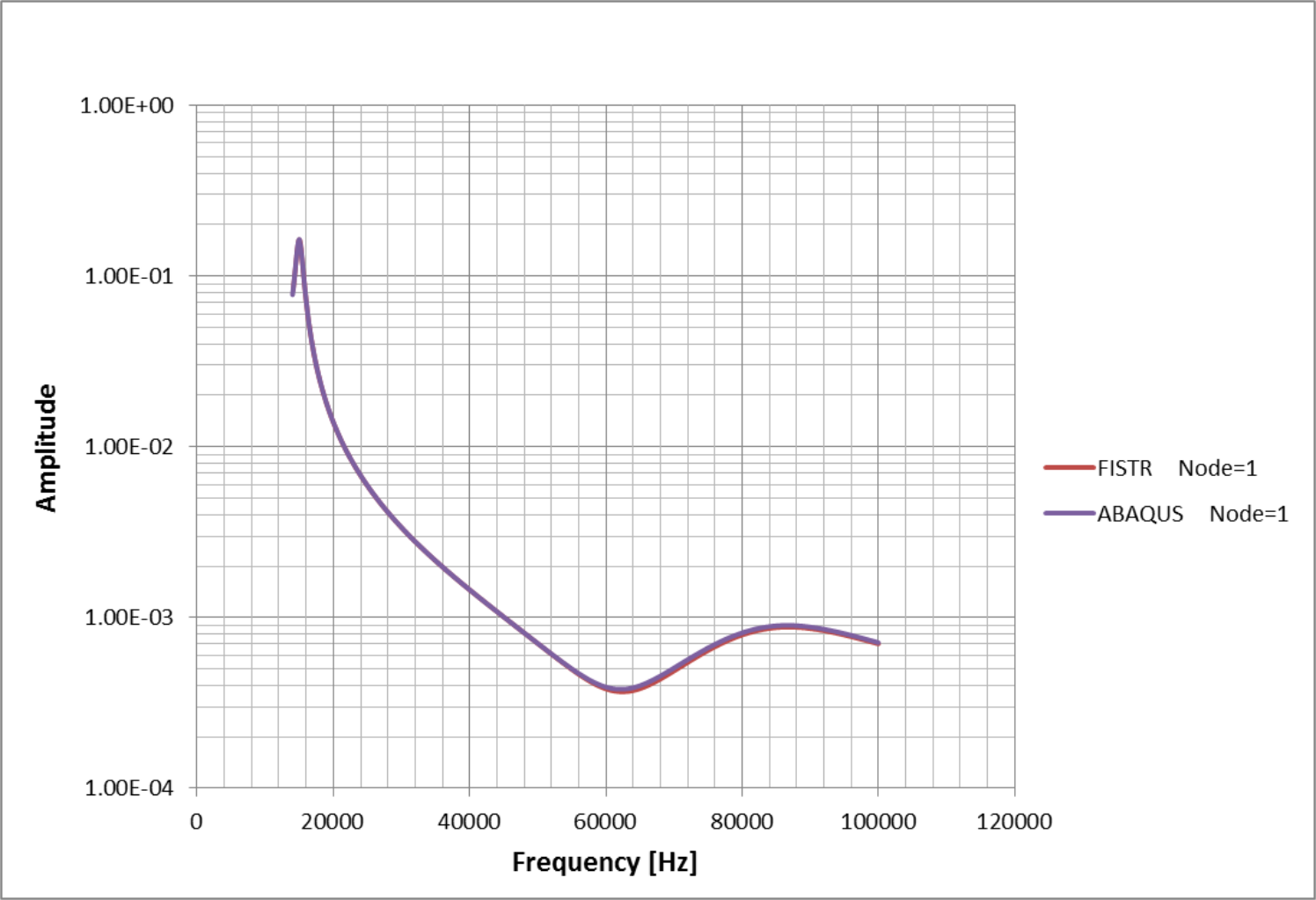
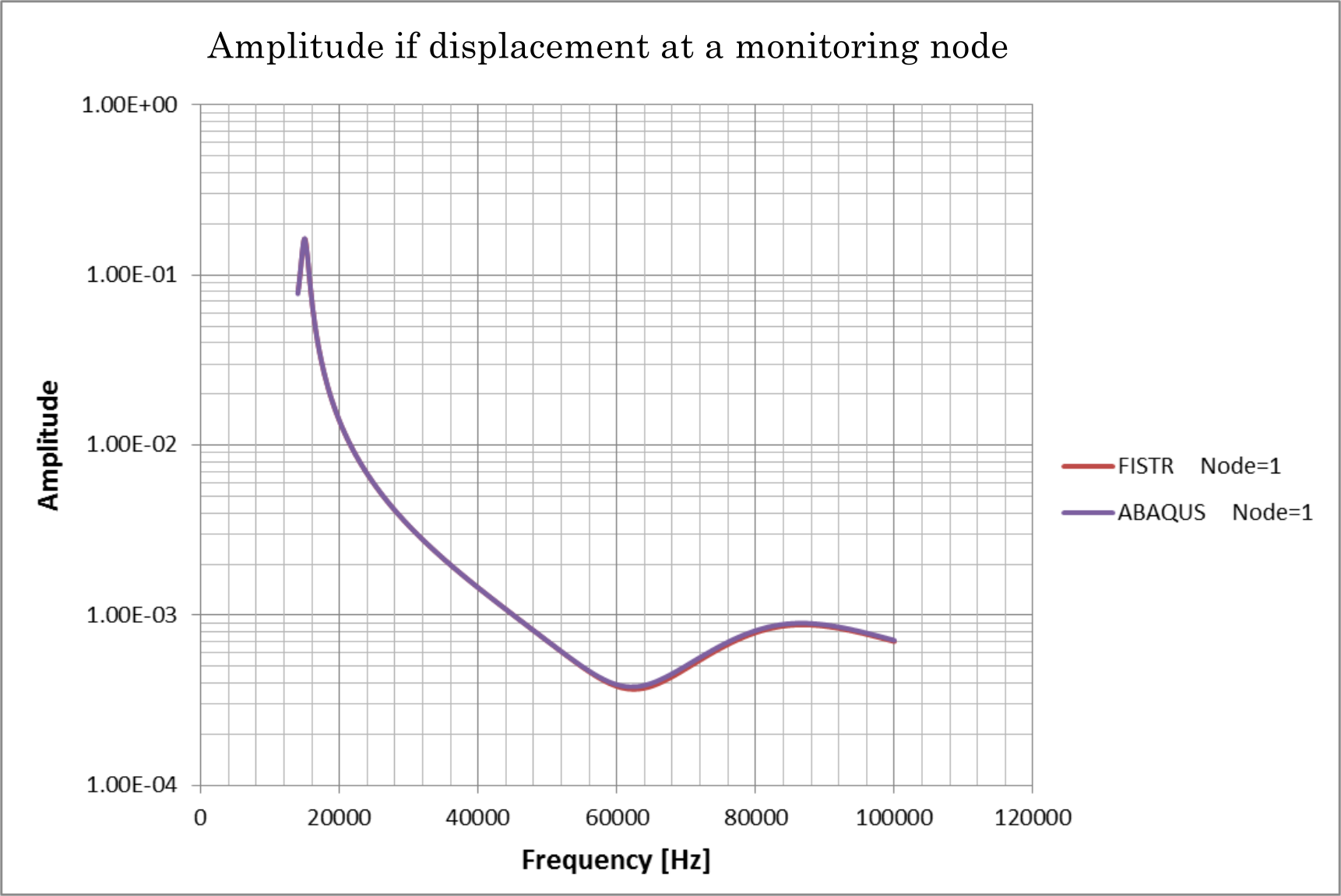
(6) Frequency response analysis

In this verification, a frequency response analysis was performed on a cantilever, and the results were compared with those obtained using the ABAQUS software. The analysis model and verification conditions are presented below:

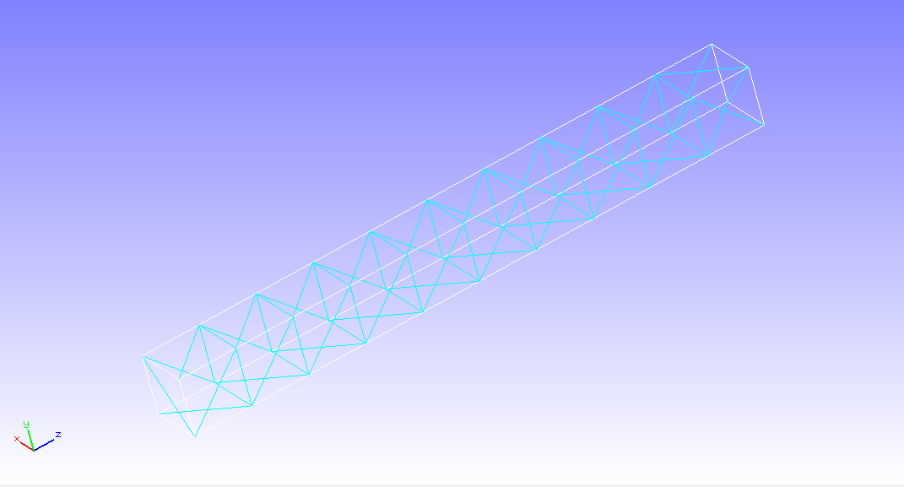
Analysis conditions:


Young's modulus	$E$	$210000\ N/mm^2$
Poisson's ratio	$\nu$	$0.3$
Density	$\rho$	$7.89E-09\ t/mm^3$
Gravitational acceleration	$g$	$9800.0\ mm/s^2$
Load	$F_0$	$1.0\ N$
Parameter of Rayleigh damping	$R_m$	$0.0$
Parameter of Rayleigh damping	$R_k$	$7.2E-07$

Fig. 9.1.15 : Analysis model (tetrahedral primary element (126 elements and 55 nodes))

The eigenvalues up to the fifth order and the frequency response of the vibration points obtained from eigenvalue analysis are as follows:

mode	FrontISTR	ABAQUS
1	14952	14952
2	15002	15003
3	84604	84539
4	84771	84697
5	127054	126852

Frequency dependence of displacement strength of vibration points

Fig. 9.1.16 : Frequency dependence of displacement strength of vibration points