Non-linear Static Analysis (Elastoplastic, Part 2)
Non-linear Static Analysis (Elastoplastic, Part 2)
This analysis uses the data of tutorial/06_plastic_can.
Analysis target
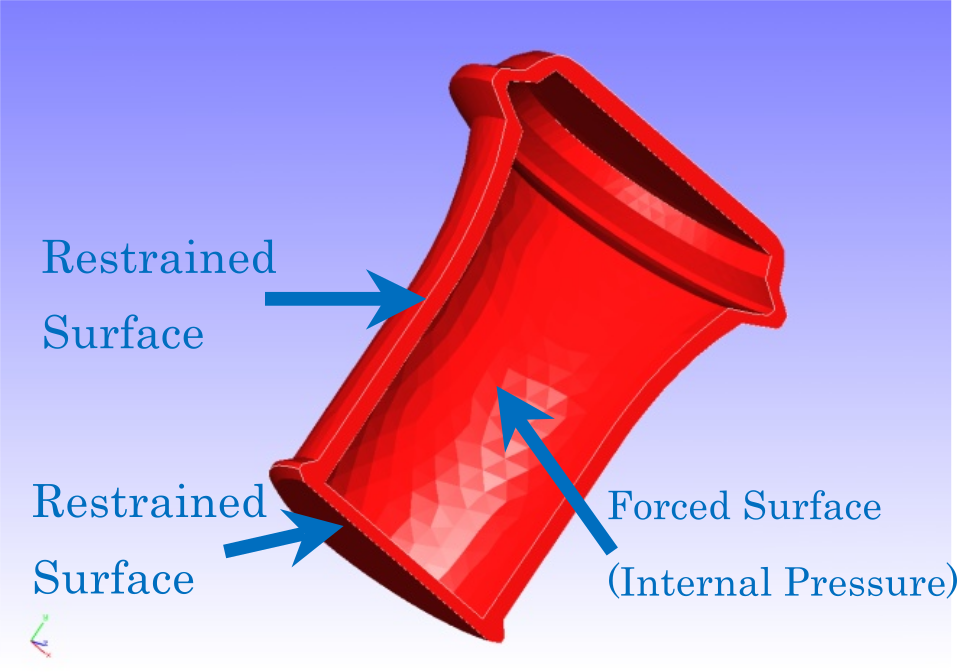
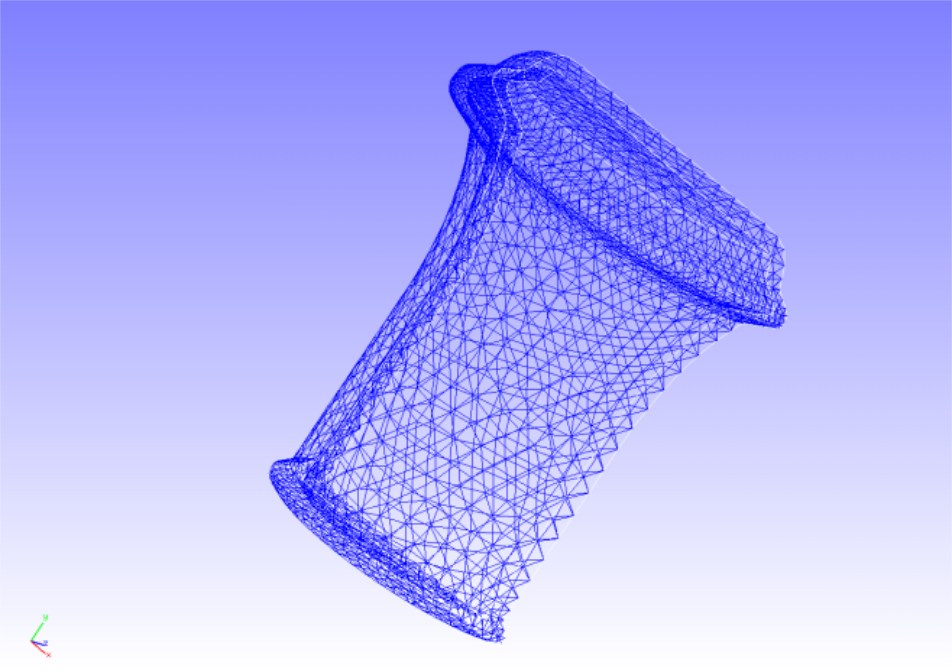
The target of this analysis is a 1/2 model of a container whose shape and mesh data are shown in Figs. 4.6.1 and 4.6.2, respectively. The mesh is a tetrahedral secondary element with 7236 elements and 14119 nodes.
| Item | Description | Notes | Reference |
|---|---|---|---|
| Type of analysis | Non-linear static analysis(plastic) | !SOLUTION,TYPE=NLSTATIC | |
| Number of nodes | 14,119 | ||
| Number of elements | 7,236 | ||
| Element type | Ten node tetrahedral quadratic element | !ELEMENT,TYPE=342 | |
| Material name | M1 | !MATERIAL,NAME=M1 | |
| Material property | ELASTIC, PLASTIC | !ELASTIC !PLASTIC,YIELD=DRACKER-PRAGER | |
| Boundary conditions | Restraint, Distribution force | !DLOAD | |
| Matrix solution | CG/SSOR | !SOLVER,METHOD=CG,PRECOND=1 |
Fig. 4.6.1: Shape of the container
Fig. 4.6.2: Mesh data of the container
Analysis content
A stress analysis is performed by restraining the displacement of the restraining surface as shown in Fig. 4.6.1 and applying distributed loads to the inside of the vessel as a forced surface. The Drucker-Prager model is used for the yield function. The analytical control data are shown below.
Analysis control data can.cnt
# Control File for FISTR
## Analysis Control
!VERSION
3
!SOLUTION, TYPE=NLSTATIC
!WRITE,RESULT
!WRITE,VISUAL
## Solver Control
### Boundary Conditon
!BOUNDARY, GRPID=1
BND0, 3, 3, 0.000000
!BOUNDARY, GRPID=1
BND1, 1, 1, 0.000000
BND1, 2, 2, 0.000000
BND1, 3, 3, 0.000000
!DLOAD, GRPID=1
DL0, S, 1.0
!DLOAD, GRPID=1
DL1, S, 1.0
!DLOAD, GRPID=1
DL2, S, 0.5
### STEP
!STEP, SUBSTEPS=10, CONVERG=1.0e-5
BOUNDARY, 1
LOAD, 1
### Material
!MATERIAL, NAME=M1
!ELASTIC
24000.0, 0.2
!PLASTIC, YIELD=DRUCKER-PRAGER
500.0, 20.0, 0.0
### Solver Setting
!SOLVER,METHOD=CG,PRECOND=1,ITERLOG=NO,TIMELOG=YES
20000, 1
1.0e-8, 1.0, 0.0
## Post Control
!VISUAL,metod=PSR
!surface_num=1
!surface 1
!output_type=VTK
!END
Analysis procedure
Execute the FrontISTR execution command fistr1.
$ cd FrontISTR/tutorial/06_plastic_can
$ fistr1 -t 4
(Runs in 4 threads.)
Analysis results
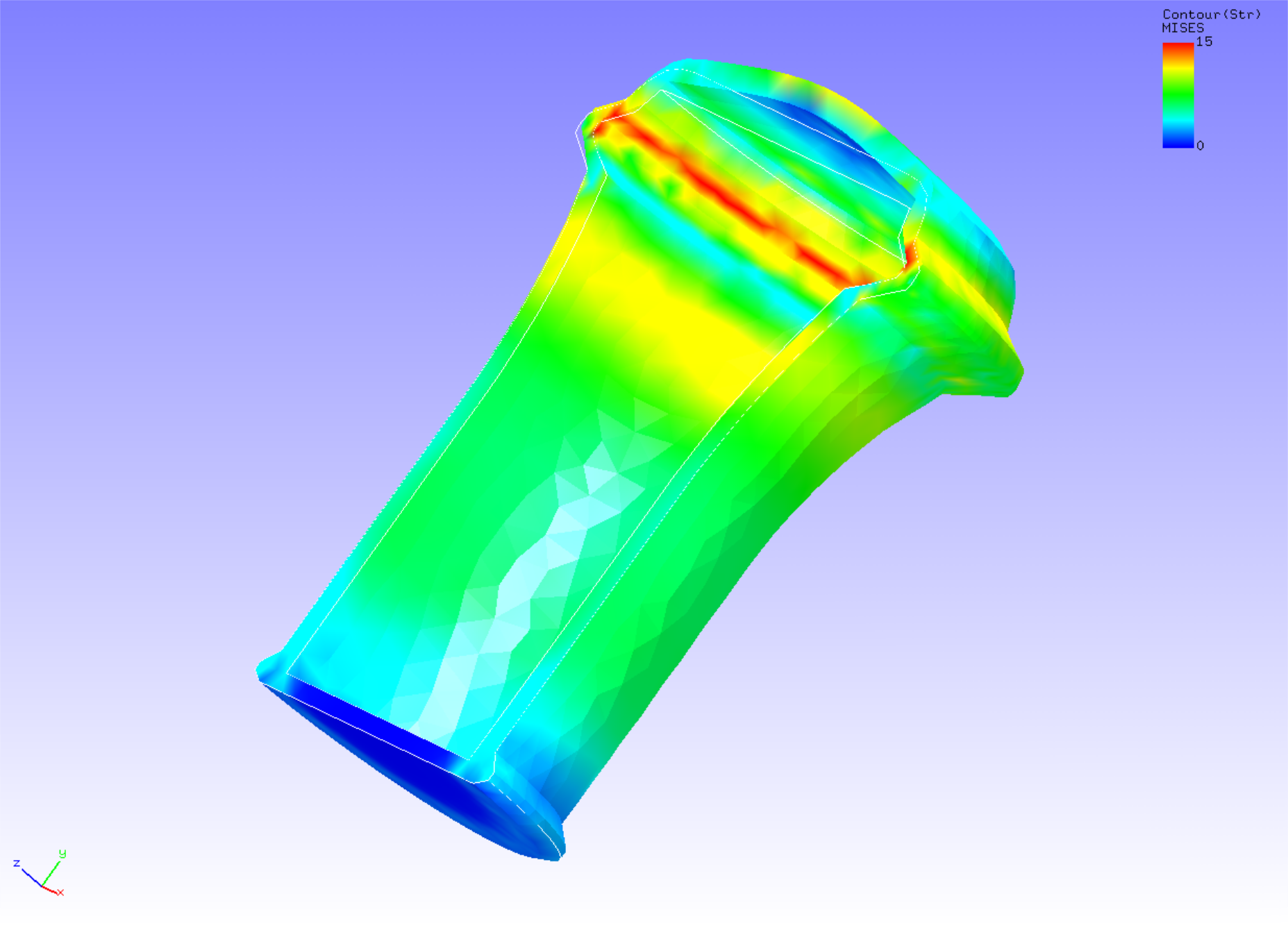
For the results of the tenth substep analysis, a deformation diagram with the Mises stress contours added is created by REVOCAP_PrePost and shown in Figure 4.6.3. The deformation factor is set to 30. A part of the log file is shown below as numerical data of the analysis results.
Fig. 4.6.3: Analysis results of deformation and Mises stress
Log file 0.log.
fstr_setup: OK
#### Result step= 0
##### Local Summary @Node :Max/IdMax/Min/IdMin####
//U1 0.0000E+00 1 0.0000E+00 1
//U2 0.0000E+00 1 0.0000E+00 1
//U3 0.0000E+00 1 0.0000E+00 1
//E11 0.0000E+00 1 0.0000E+00 1
//E22 0.0000E+00 1 0.0000E+00 1
//E33 0.0000E+00 1 0.0000E+00 1
//E12 0.0000E+00 1 0.0000E+00 1
//E23 0.0000E+00 1 0.0000E+00 1
//E31 0.0000E+00 1 0.0000E+00 1
//S11 0.0000E+00 1 0.0000E+00 1
//S22 0.0000E+00 1 0.0000E+00 1
//S33 0.0000E+00 1 0.0000E+00 1
//S12 0.0000E+00 1 0.0000E+00 1
//S23 0.0000E+00 1 0.0000E+00 1
//S31 0.0000E+00 1 0.0000E+00 1
//SMS 0.0000E+00 1 0.0000E+00 1
##### Local Summary @Element :Max/IdMax/Min/IdMin####
//E11 0.0000E+00 1 0.0000E+00 1
//E22 0.0000E+00 1 0.0000E+00 1
//E33 0.0000E+00 1 0.0000E+00 1
//E12 0.0000E+00 1 0.0000E+00 1
//E23 0.0000E+00 1 0.0000E+00 1
//E31 0.0000E+00 1 0.0000E+00 1
//S11 0.0000E+00 1 0.0000E+00 1
//S22 0.0000E+00 1 0.0000E+00 1
//S33 0.0000E+00 1 0.0000E+00 1
//S12 0.0000E+00 1 0.0000E+00 1
//S23 0.0000E+00 1 0.0000E+00 1
//S31 0.0000E+00 1 0.0000E+00 1
//SMS 0.0000E+00 1 0.0000E+00 1
##### Global Summary @Node :Max/IdMax/Min/IdMin####
//U1 0.0000E+00 1 0.0000E+00 1
//U2 0.0000E+00 1 0.0000E+00 1
//U3 0.0000E+00 1 0.0000E+00 1
//E11 0.0000E+00 1 0.0000E+00 1
//E22 0.0000E+00 1 0.0000E+00 1
//E33 0.0000E+00 1 0.0000E+00 1
//E12 0.0000E+00 1 0.0000E+00 1
//E23 0.0000E+00 1 0.0000E+00 1
//E31 0.0000E+00 1 0.0000E+00 1
//S11 0.0000E+00 1 0.0000E+00 1
//S22 0.0000E+00 1 0.0000E+00 1
//S33 0.0000E+00 1 0.0000E+00 1
//S12 0.0000E+00 1 0.0000E+00 1
//S23 0.0000E+00 1 0.0000E+00 1
//S31 0.0000E+00 1 0.0000E+00 1
//SMS 0.0000E+00 1 0.0000E+00 1
##### Global Summary @Element :Max/IdMax/Min/IdMin####
//E11 0.0000E+00 1 0.0000E+00 1
//E22 0.0000E+00 1 0.0000E+00 1
//E33 0.0000E+00 1 0.0000E+00 1
//E12 0.0000E+00 1 0.0000E+00 1
//E23 0.0000E+00 1 0.0000E+00 1
//E31 0.0000E+00 1 0.0000E+00 1
//S11 0.0000E+00 1 0.0000E+00 1
//S22 0.0000E+00 1 0.0000E+00 1
//S33 0.0000E+00 1 0.0000E+00 1
//S12 0.0000E+00 1 0.0000E+00 1
//S23 0.0000E+00 1 0.0000E+00 1
//S31 0.0000E+00 1 0.0000E+00 1
//SMS 0.0000E+00 1 0.0000E+00 1
...
#### Result step= 10
##### Local Summary @Node :Max/IdMax/Min/IdMin####
//U1 1.6169E+00 1600 -1.6123E+00 11901
//U2 1.9281E+01 6877 -4.5296E-01 7096
//U3 1.6087E+00 7016 -1.5107E+00 6934
//E11 9.9108E-04 11242 -6.5834E-04 1404
//E22 1.5025E-03 13972 -5.4245E-04 2367
//E33 9.8320E-04 6833 -6.4744E-04 7000
//E12 1.6822E-03 2698 -1.7175E-03 11906
//E23 1.7082E-03 6749 -1.4469E-03 13509
//E31 1.2090E-03 12475 -1.1181E-03 11342
//S11 2.7781E+01 1086 -1.9439E+01 2363
//S22 3.7876E+01 13972 -1.4556E+01 2367
//S33 2.7335E+01 1086 -1.9745E+01 13082
//S12 1.6817E+01 2698 -1.7170E+01 11906
//S23 1.7077E+01 6749 -1.4463E+01 13509
//S31 1.2086E+01 12475 -1.1178E+01 11342
//SMS 3.7448E+01 2834 2.7593E-04 7333
##### Local Summary @Element :Max/IdMax/Min/IdMin####
//E11 5.8557E-04 6613 -4.0802E-04 6416
//E22 1.1391E-03 7144 -3.1424E-04 6613
//E33 6.9233E-04 6130 -4.5897E-04 6222
//E12 1.1076E-03 165 -1.1101E-03 5196
//E23 1.4338E-03 6215 -9.2107E-04 6176
//E31 9.6618E-04 5618 -7.4939E-04 4704
//S11 1.7994E+01 6613 -1.2254E+01 6224
//S22 2.7863E+01 7144 -7.3017E+00 24
//S33 1.9725E+01 6613 -1.3385E+01 6222
//S12 1.1072E+01 165 -1.1097E+01 5196
//S23 1.4332E+01 6215 -9.2080E+00 6176
//S31 9.6603E+00 5618 -7.4918E+00 4704
//SMS 3.3151E+01 5619 3.3306E-04 2665
##### Global Summary @Node :Max/IdMax/Min/IdMin####
//U1 1.6169E+00 1600 -1.6123E+00 11901
//U2 1.9281E+01 6877 -4.5296E-01 7096
//U3 1.6087E+00 7016 -1.5107E+00 6934
//E11 9.9108E-04 11242 -6.5834E-04 1404
//E22 1.5025E-03 13972 -5.4245E-04 2367
//E33 9.8320E-04 6833 -6.4744E-04 7000
//E12 1.6822E-03 2698 -1.7175E-03 11906
//E23 1.7082E-03 6749 -1.4469E-03 13509
//E31 1.2090E-03 12475 -1.1181E-03 11342
//S11 2.7781E+01 1086 -1.9439E+01 2363
//S22 3.7876E+01 13972 -1.4556E+01 2367
//S33 2.7335E+01 1086 -1.9745E+01 13082
//S12 1.6817E+01 2698 -1.7170E+01 11906
//S23 1.7077E+01 6749 -1.4463E+01 13509
//S31 1.2086E+01 12475 -1.1178E+01 11342
//SMS 3.7448E+01 2834 2.7593E-04 7333
##### Global Summary @Element :Max/IdMax/Min/IdMin####
//E11 5.8557E-04 6613 -4.0802E-04 6416
//E22 1.1391E-03 7144 -3.1424E-04 6613
//E33 6.9233E-04 6130 -4.5897E-04 6222
//E12 1.1076E-03 165 -1.1101E-03 5196
//E23 1.4338E-03 6215 -9.2107E-04 6176
//E31 9.6618E-04 5618 -7.4939E-04 4704
//S11 1.7994E+01 6613 -1.2254E+01 6224
//S22 2.7863E+01 7144 -7.3017E+00 24
//S33 1.9725E+01 6613 -1.3385E+01 6222
//S12 1.1072E+01 165 -1.1097E+01 5196
//S23 1.4332E+01 6215 -9.2080E+00 6176
//S31 9.6603E+00 5618 -7.4918E+00 4704
//SMS 3.3151E+01 5619 3.3306E-04 2665