Frequency Response Analysis
Frequency Response Analysis
This analysis uses the data of tutorial/17_freq_beam.
Analysis target
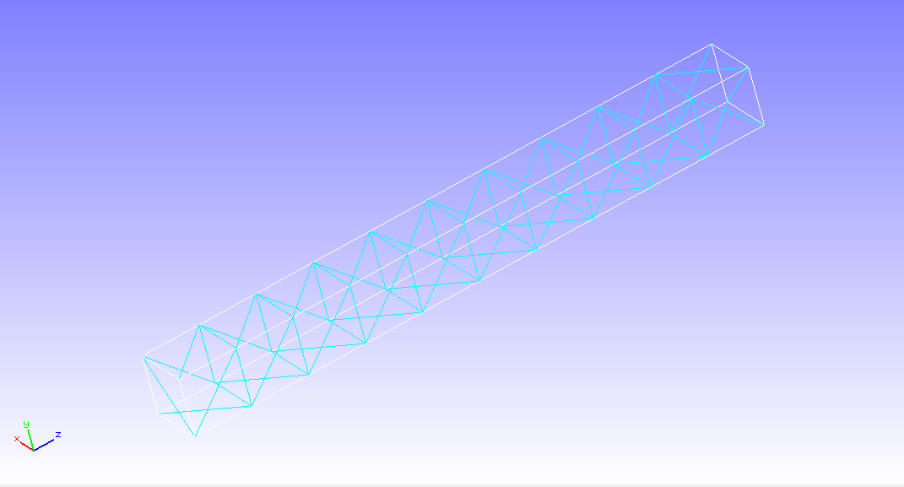
The analysis target is a cantilevered beam, and the geometry is shown in Figure 4.17.1 and the mesh data is shown in Figure 4.17.2.
| Item | Description | Notes | Reference |
|---|---|---|---|
| Type of analysis | Frequency response analysis | !SOLUTION,TYPE=EIGEN !SOLUTION,TYPE=DYNAMIC | |
| Number of nodes | 55 | ||
| Number of elements | 126 | ||
| Element type | Four node tetrahedral element | !ELEMENT,TYPE=341 | |
| Material name | Material-1 | !MATERIAL,NAME=Material-1 | |
| Boundary conditions | Restraint, Concentrated force, eigen value | !EIGENREAD | |
| Matrix solution | CG/SSOR | !SOLVER,METHOD=CG,PRECOND=1 |

Analysis content
The end of a cantilevered beam to be analyzed is fully constrained, and a frequency response analysis is performed by applying concentrated loads to two nodes at the opposite end.
After analyzing eigenvalues up to the 10th order under the same boundary conditions, the analysis is performed using eigenvalues and eigenvectors up to the 5th order. The analysis control data for frequency response analysis is shown below.
Analysis control data beam_eigen.cnt.
# Control File for FISTR
!VERSION
3
!WRITE,RESULT
!WRITE,VISUAL
!SOLUTION, TYPE=EIGEN
!EIGEN
10, 1.0E-8, 60
!BOUNDARY
_PickedSet4, 1, 3, 0.0
!SOLVER,METHOD=CG,PRECOND=1,ITERLOG=NO,TIMELOG=YES
10000, 1
1.0e-8, 1.0, 0.0
!VISUAL,metod=PSR
!surface_num=1
!surface 1
!output_type=VTK
!END
Analysis control data beam_freq.cnt.
# Control File for FISTR
!VERSION
3
!WRITE,RESULT
!WRITE,VISUAL
!SOLUTION, TYPE=DYNAMIC
!DYNAMIC
11 , 2
14000, 16000, 20, 15000.0
0.0, 6.6e-5
1, 1, 0.0, 7.2E-7
10, 2, 1
1, 1, 1, 1, 1, 1
!EIGENREAD
eigen_0.log
1, 5
!BOUNDARY
_PickedSet4, 1, 3, 0.0
!FLOAD, LOAD CASE=2
_PickedSet5, 2, 1.
!FLOAD, LOAD CASE=2
_PickedSet6, 2, 1.
!SOLVER,METHOD=CG,PRECOND=1,ITERLOG=NO,TIMELOG=YES
10000, 1
1.0e-8, 1.0, 0.0
!VISUAL,metod=PSR
!surface_num=1
!surface 1
!output_type=VTK
!END
Analysis procedure
First, change hecmw_ctrl_eigen.dat to hecmw_ctrl.dat for eigenvalue analysis, and then run eigenvalue analysis.
Next, change hecmw_ctrl_freq.dat to hecmw_ctrl.dat and 0.log to eigen_0.log (which is specified in the control data for frequency response analysis), and then perform the frequency response analysis.
$ cp hecmw_ctrl_eigen.dat hecmw_ctrl.dat
$ fistr1 -t 4
$ mv 0.log eigen_0.log
$ cp hecmw_ctrl_freq.dat hecmw_ctrl.dat
$ fistr1 -t 4
Analysis results
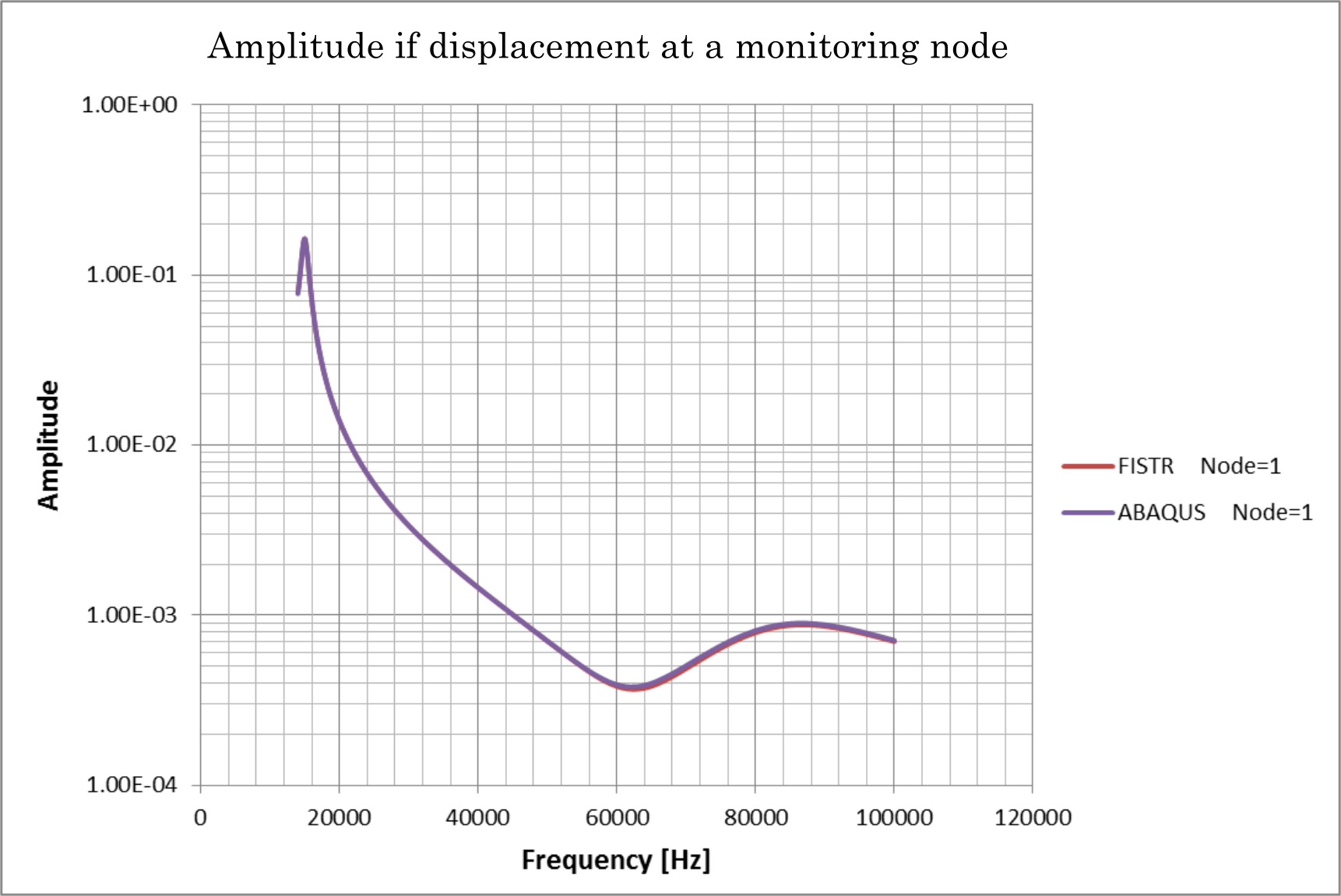
The relationship between the frequency and displacement amplitude of a monitoring node (node number 1) specified in the analysis control data is shown in Figure 4.17.3, created using Microsoft Excel. A part of the analysis result log file is shown below as numerical data for the analysis results.
Log file 0.log
fstr_setup: OK
Rayleigh alpha: 0.0000000000000000
Rayleigh beta: 7.1999999999999999E-007
read from=eigen_0.log
start mode= 1
end mode= 5
start frequency: 14000.000000000000
end frequency: 16000.000000000000
number of the sampling points 20
monitor nodeid= 1
14100.000000000000 [Hz] : 8.3935554529723885E-002
14100.000000000000 [Hz] : 1 .res
14200.000000000000 [Hz] : 9.1211083509607632E-002
14200.000000000000 [Hz] : 2 .res
14300.000000000000 [Hz] : 9.9579777896922961E-002
14300.000000000000 [Hz] : 3 .res
14400.000000000000 [Hz] : 0.10914967594967491
14400.000000000000 [Hz] : 4 .res
14500.000000000000 [Hz] : 0.11992223203326918
14500.000000000000 [Hz] : 5 .res
14600.000000000000 [Hz] : 0.13164981801806747
14600.000000000000 [Hz] : 6 .res
14700.000000000000 [Hz] : 0.14360931008440975
14700.000000000000 [Hz] : 7 .res
14800.000000000000 [Hz] : 0.15436500205940235
14800.000000000000 [Hz] : 8 .res
14900.000000000000 [Hz] : 0.16180768408076251
14900.000000000000 [Hz] : 9 .res
15000.000000000000 [Hz] : 0.16388019610373711
15000.000000000000 [Hz] : 10 .res
15100.000000000000 [Hz] : 0.15982110598747551
15100.000000000000 [Hz] : 11 .res
15200.000000000000 [Hz] : 0.15074650286398145
15200.000000000000 [Hz] : 12 .res
15300.000000000000 [Hz] : 0.13885370598993371
15300.000000000000 [Hz] : 13 .res
15400.000000000000 [Hz] : 0.12618976409021948
15400.000000000000 [Hz] : 14 .res
15500.000000000000 [Hz] : 0.11405716994112736
15500.000000000000 [Hz] : 15 .res
15600.000000000000 [Hz] : 0.10306231010139058
15600.000000000000 [Hz] : 16 .res
15700.000000000000 [Hz] : 9.3374567545990342E-002
15700.000000000000 [Hz] : 17 .res
15800.000000000000 [Hz] : 8.4945897112663621E-002
15800.000000000000 [Hz] : 18 .res
15900.000000000000 [Hz] : 7.7641947016103510E-002
15900.000000000000 [Hz] : 19 .res
16000.000000000000 [Hz] : 7.1307642422355627E-002
16000.000000000000 [Hz] : 20 .res
start time: 0.0000000000000000
end time: 6.6000000000000005E-005
frequency: 15000.000000000000
node id: 1
num disp: 10
time= 0.0000000000000000 : 1 .res
time= 0.0000000000000000 : 1 .vis
time= 6.6000000000000003E-006 : 2 .res
time= 6.6000000000000003E-006 : 2 .vis
time= 1.3200000000000001E-005 : 3 .res
time= 1.3200000000000001E-005 : 3 .vis
time= 1.9800000000000000E-005 : 4 .res
time= 1.9800000000000000E-005 : 4 .vis
time= 2.6400000000000001E-005 : 5 .res
time= 2.6400000000000001E-005 : 5 .vis
time= 3.3000000000000003E-005 : 6 .res
time= 3.3000000000000003E-005 : 6 .vis
time= 3.9600000000000000E-005 : 7 .res
time= 3.9600000000000000E-005 : 7 .vis
time= 4.6200000000000005E-005 : 8 .res
time= 4.6200000000000005E-005 : 8 .vis
time= 5.2800000000000003E-005 : 9 .res
time= 5.2800000000000003E-005 : 9 .vis
time= 5.9400000000000000E-005 : 10 .res
time= 5.9400000000000000E-005 : 10 .vis