Eigenvalue Analysis

This analysis uses the data of tutorial/15_eigen_spring.

Analysis target

The objects of analysis are the same springs as in the Non-linear Static Analysis (Hyperelasticity, Part 2) in the previous section.

Item	Description	Notes
Type of analysis	Eigen value analysis	!SOLUTION,TYPE=EIGEN
Number of nodes	78,771
Number of elements	46,454
Element type	Ten node tetrahedral quadratic element	!ELEMENT,TYPE=342
Material name	MAT1	!MATERIAL,NAME=MAT1
Boundary conditions	Restraint
Matrix solution	Direct method	!SOLVER,METHOD=DIRECT

Analysis content

The displacements of the constrained surfaces shown in Figure 4.4.1 are constrained, and eigenvalue analysis is performed up to the fifth order. The analysis control data is shown below.

Analysis control data `spring.cnt`.

#  Control File for FISTR
## Analysis Control
!VERSION
 3
!SOLUTION, TYPE=EIGEN
!EIGEN
 5, 1.0E-8, 60
!WRITE,RESULT
!WRITE,VISUAL
## Solver Control
### Boundary Conditon
!BOUNDARY
 XFIX, 1, 1, 0.0
 YFIX, 2, 2, 0.0
 ZFIX, 3, 3, 0.0
### Material
# define in mesh file
### Solver Setting
!SOLVER,METHOD=DIRECT
## Post Control
!VISUAL,metod=PSR
!surface_num=1
!surface 1
!output_type=VTK
!END

Analysis procedure

Execute the FrontISTR execution command fistr1.

$ cd FrontISTR/tutorial/15_eigen_spring
$ fistr1 -t 4
(Runs in 4 threads.)

Analysis results

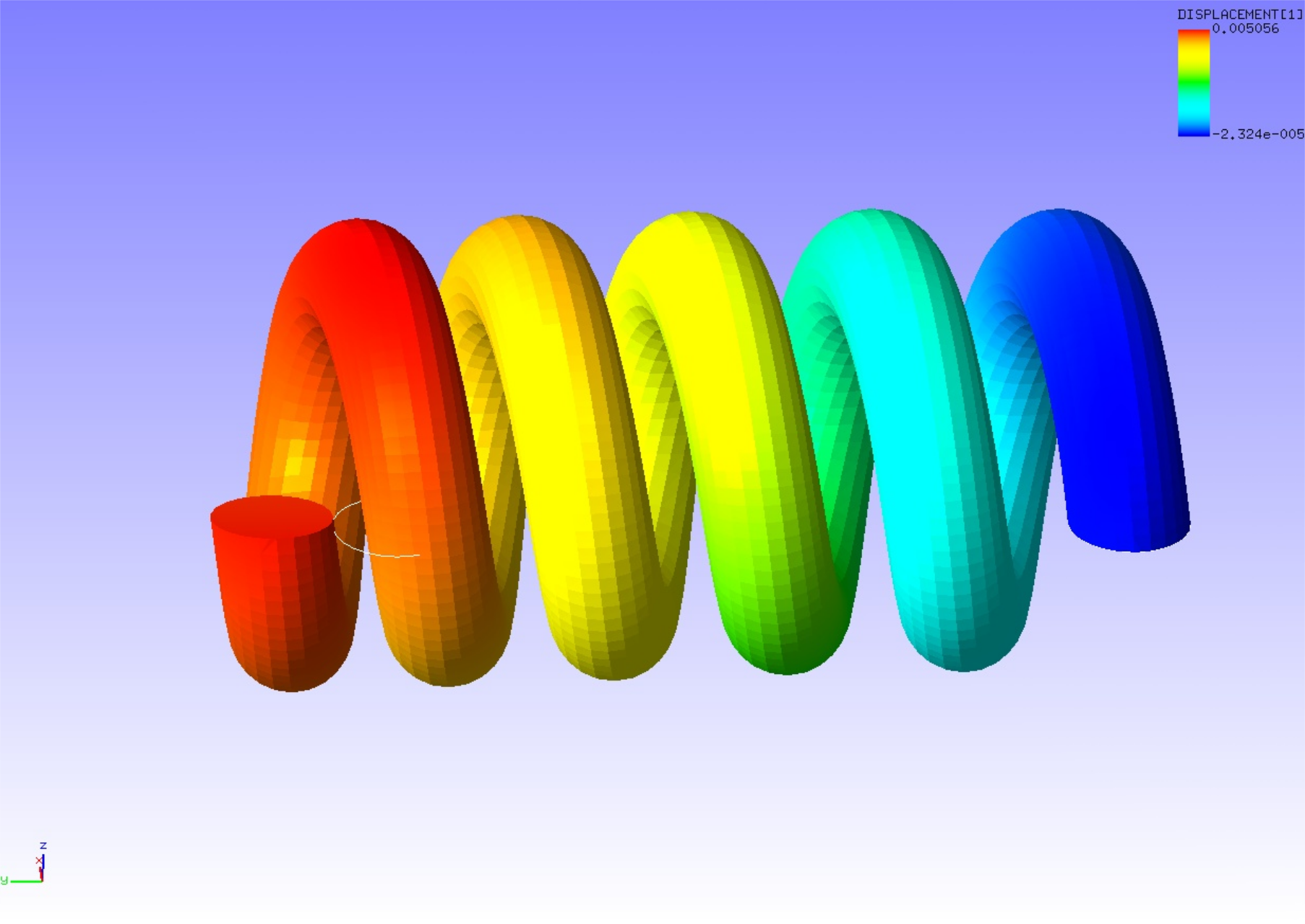
Using the resulting data file spring.res.0.3, the third order vibration mode (compression and extension of the spring in the y direction) is created by REVOCAP_PrePost and shown in Figure 4.15.1. The deformation factor is set to 1000. In addition, a list of natural frequencies output to the analysis results log file is shown below as numerical data for the analysis results.

Third vibration mode of a spring

Fig. 4.15.1: Third vibration mode of a spring

Log file `0.log`.

 fstr_setup: OK

********************************
*RESULT OF EIGEN VALUE ANALYSIS*
********************************

NUMBER OF ITERATIONS =       47
TOTAL MASS =   3.4184E-06

                   ANGLE       FREQUENCY   PARTICIPATION FACTOR                EFFECTIVE MASS
  NO.  EIGENVALUE  FREQUENCY   (HZ)        X           Y           Z           X           Y           Z
  ---  ----------  ----------  ----------  ----------  ----------  ----------  ----------  ----------  ----------
    1  7.8307E+06  2.7983E+03  4.4537E+02  1.0289E+00 -8.8939E-02 -7.0520E-01  1.3006E-06  9.7176E-09  6.1094E-07
    2  7.8716E+06  2.8056E+03  4.4653E+02  6.9687E-01  1.0755E-01  1.0106E+00  6.1290E-07  1.4598E-08  1.2890E-06
    3  3.2600E+07  5.7097E+03  9.0872E+02  4.8622E-03  1.2364E+00 -7.9172E-02  4.0069E-11  2.5908E-06  1.0624E-08
    4  3.8366E+07  6.1940E+03  9.8581E+02 -2.9654E-02  3.3849E-01 -6.7819E-03  9.8232E-10  1.2799E-07  5.1379E-11
    5  1.2931E+08  1.1372E+04  1.8098E+03  5.1856E-01  4.7604E-02  6.7703E-01  2.8377E-07  2.3915E-09  4.8371E-07

    Iter.#   Eigenvalue    Abs. Residual
    1  7.8307E+06  9.2347E-09
    2  7.8716E+06  7.8593E-08
    3  3.2600E+07  1.0084E-07
    4  3.8366E+07  5.3113E-08
    5  1.2931E+08  6.8762E-08

Eigenvalue Analysis